1

I am trying to program a binomial tree in Matlab. The tree looks something like this:

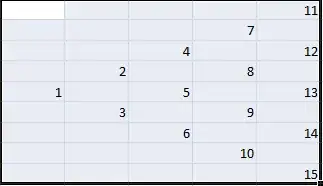
enter image description here

The numbers in the picture refer to the index of the array to create a binomial tree.

Problem:

Value of 2 = 0.5*Value of 4 + 0.5*Value of 5

Value of 3 = 0.5*Value of 5 + 0.5*Value of 6

I need to link the value of 2 to value of 4 and value of 5, similarly for value of 3 accordingly.

How do i get the link mathematically so that I can program it, instead of stating it manually?

I hope the problem is clear. Need some guidance on this.

How I am programming it?

Basically I am trying to model an interest rate tree. I am having a array for interest and another for the discounted value. I have a previous qn:Interest Rate Tree in Matlab. Now I am changing to vectors.I programmed it using cell arrays, now changing to vectors.

Interest = [0.03;0;0];
DiscountedValue =zeros(3,1);

Interest = [Interest; zeros(n,1)];
DiscountedValue = [DiscountedValue; zeros(n,1)];

total= size(Interest,1);
DiscountedValue(end:-1:(end-n+1)) = 100;
m=0
for i=total-n:-1:total-2n+2
        Interest(i)= (alpha*exp(2^(m)*volatility))/100;
        m = m+1;
end
for j= total-n:-1:1
    //Stuck here//DiscountedValue(j) = (0.5*DiscountedValue(j+0.5*DiscountedValue{j+1}(2,i+1))/(1+Interest(j));
end
Community
  • 1
lakshmen
  • 1,005
  • 1
    You need to separate $5$ from $3$ since what you have now isn't a binomial tree. Child nodes are not shared between parent nodes. – John Habert Feb 08 '14 at 20:20
  • @JohnHabert good spot, I was writing an answer based on a binary tree and was about to post it and noticed my formula didn't work... – TooTone Feb 08 '14 at 20:22
  • @JohnHabert True isn't a binary tree or any kind of tree, but it does sound like a reasonable DAG that might reasonably be described as "binomial" (in reference to Pascal's triangle). I ask the OP to clarify this. – Erick Wong Feb 08 '14 at 20:22
  • However this is a binomial (not binary) tree as used in finance for calculating prices of assets that depend upon other assets. – TooTone Feb 08 '14 at 20:23
  • @TooTone yes i am trying to model the a binomial tree in finance... – lakshmen Feb 08 '14 at 20:23
  • @lakesh What you probably want is a simple way to convert back and forth between indices and column/position coordinates. E.g. 3 is located in the position 2 of column 2, and its children are positions 2 and 3 of column 3. This isn't hard at least in one direction...have you given thought to this approach? – Erick Wong Feb 08 '14 at 20:24
  • @ErickWong I just showed a example. It was in Excel to simplify things. But I am using arrays to program it. Need some link between them. I have given thought but it wasn't working.. – lakshmen Feb 08 '14 at 20:25
  • Guess I was wrong about binomial tree. I'm used to trees from math and CS not business. – John Habert Feb 08 '14 at 20:27
  • @lakesh Can you give a little more detail about how you are programming this? Single array for the whole tree? Are calculations done top (left in your picture) to bottom (right) or bottom to top? – John Habert Feb 08 '14 at 20:28
  • @JohnHabert Sure. Just a sec... – lakshmen Feb 08 '14 at 20:29
  • @lakesh You could use lookup tables. I.e. two more arrays of the same size to contain the indices of the upper and lower children. – TooTone Feb 08 '14 at 20:33
  • @TooTone I don't think i can use that because I still need to optimize the values in the cell.. – lakshmen Feb 08 '14 at 20:35

2 Answers2

3

The bottom numbers on your columns are the triangular numbers $\frac 12n(n+1)$ where $n$ is the column number. If you have a number, say $5$, the number up and to the right is $5+n$, where $n$ is the column number of $5$ and the number down and to the right is $5+n+1$. We will be done if we can find the column number from the entry.

Given a triangular number $m$, its column number is the $n$ such that $m=\frac 12n(n+1)$ or $n^2+n-2m=0$ We can use the quadratic formula to solve this: $n=\frac 12(-1+\sqrt{1+8m})$ So given an entry $m$ in your triangle, its column number is $\lceil \frac 12(-1+\sqrt{1+8m}) \rceil$

For a test, let $m=13$. It column number is $\lceil \frac 12(-1+\sqrt {1+8\cdot 13})=\lceil \frac 12(\sqrt{105}-1 )\rceil=\lceil \frac 12(10.25-1) \rceil =5$ and the numbers next to it are $18,19$

Ross Millikan
  • 374,822
  • is it Sqrt(105) and 0.5(sqrt(105)-1) = 4.62. How did u get 5? – lakshmen Feb 08 '14 at 20:47
  • The ceiling brackets tell you to round up to the next integer. – Ross Millikan Feb 08 '14 at 20:50
  • ok thanks alot... – lakshmen Feb 08 '14 at 20:51
  • one more qn, how do u find the parent node of a recombining tree? do u any have idea? – lakshmen Feb 11 '14 at 17:20
  • Which is the parent node of 13? – Ross Millikan Feb 11 '14 at 17:25
  • both 8 and 9 are parents... need your guidance on finding the parent node... – lakshmen Feb 11 '14 at 17:28
  • You get the parent above by subtracting the column number and the parent below by adding 1 to that. You can detect that there is not a parent below by the fact that the round up isn't necessary-that the square root comes out even. Equivalently you can check that $m=\frac 12n(n+1)$ You can detect that there is no parent above if $m=\frac12(n-1)n+1$ because it is one more than a triangular number – Ross Millikan Feb 11 '14 at 17:37
  • can show an example, didn't really get u... – lakshmen Feb 11 '14 at 17:44
  • As above, let $m=13$. We calculate $n=5$ as the column number. The parents are $13-5=8, 13-5+1=9$ If we had $m=15$, we could then notice that $m=\frac 125\cdot 6$, so it is at the bottom of the column and has no lower parent. If $m=11,$ we find $m=\frac 12(5-1)\cdot 5+1$, so we are at the top of a column and there is no upper parent – Ross Millikan Feb 11 '14 at 17:50
  • Thanks a lot. Btw i posted a qn called parent node of recombining tree. Add yours an answer there, I will upvote for u. – lakshmen Feb 11 '14 at 18:07
0

I'm not sure if I understood your question quite well, but you may want to consider this "trick" in order to get the coefficients of the Pascal's triangle.

Consider the matrix whose elements are given by:

$$a_{ij} = \left\{\begin{array}{ll} 0 & i \neq j-1\\ i-1 & i = j-1 \end{array}\right.$$

Compute now the exponential matrix, $M = e^A$, and note that the non-zero elements of the $i$th row of $M$ (wich is a lower triangle matrix) is the $i$th row of the Pascal's triangle.

Example

If $$A = \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \end{array} \right),$$

then

$$M = e^{A} = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 2 & 1 & 0 \\ 1 & 3 & 3 & 1 \end{array} \right). $$

The matrix exponential in Matlab is computed with expm.

Cheers!

Source here. Search for the t-shirt answer given by @Gottfried Helms.

Community
  • 1
Dmoreno
  • 7,517