0

I have posted an earlier question: Finding the child node in the recombining binomial tree. Now I would like to find the parent of a node in recombining tree.

The tree looks like this:

I

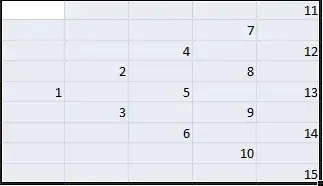
Now I need to find that the node of $4$ has parent as $2$ and node of $5$ has a parent of both $2$ and $3$.

Using the answer given in Finding the child node qn, I can find the parents of $5$ in this way: $$⌈\dfrac{1}{2}*(−1+\sqrt{1+8*5})⌉=3-1$$(which is basically to remove from $5$ the columnnumber from previous row which is $2$) to get $3$ and $-1$ to get $2$. But the problem is for the nodes at the corner such as $4$ and $6$. Not sure how to get them.

Need some guidance on this.

Community
  • 1
lakshmen
  • 1,005

1 Answers1

1

If the node is $m$, the column it is in is $n=\left\lceil \frac 12(-1+\sqrt{1+8m})\right\rceil$ The parents of $m$ are then $m-n, m-n+1$ if they are present. There will be no lower parent if $m=\frac 12n(n+1)$ as it is the bottom of the column. There will be no upper parent if $m=\frac12(n-1)n+1$ as it will be the top of the column.

Ross Millikan
  • 374,822