Inside an equilateral triangle $ABC$,an arbitrary point $P$ is taken from which the perpendiculars $PD,PE$ and $PF$ are dropped onto the sides $BC,CA$ and $AB$,respectively.Show that the ratio $\dfrac{PD+PE+PF}{BD+CE+AF}$ does not depend upon the choice of the point $P$ and find its value.
I have no idea how to proceed. I could not do anything beyond calculating the area of $PDB,PCE,PFA$ but here I get nothing. Please help!
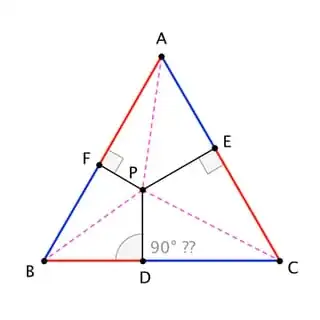
For simplicity, let the sides of the triangle be $1$.
$\hspace{3.5cm}$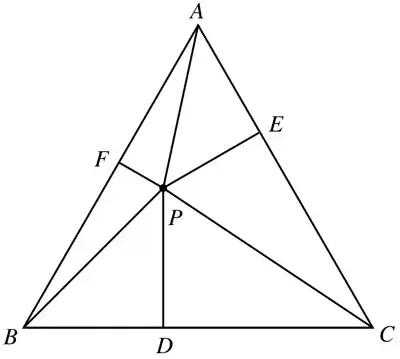
Looking at the areas of the sub-triangles, we get $$ \begin{align} |\,\triangle ABP\,|&=\frac12|\,\overline{FP}\,|\times|\,\overline{AB}\,|=\frac12|\,\overline{FP}\,|\\ |\,\triangle BCP\,|&=\frac12|\,\overline{DP}\,|\times|\,\overline{BC}\,|=\frac12|\,\overline{DP}\,|\tag{1}\\ |\,\triangle CAP\,|&=\frac12|\,\overline{EP}\,|\times|\,\overline{CA}\,|=\frac12|\,\overline{EP}\,| \end{align} $$ Summing these, we get $$ |\,\overline{FP}\,|+|\,\overline{DP}\,|+|\,\overline{EP}\,|=2|\,\triangle ABC\,|=\frac{\sqrt3}{2}\tag{2} $$
Rename the distances in question as $x$, $y$, and $z$.
$\hspace{2.3cm}$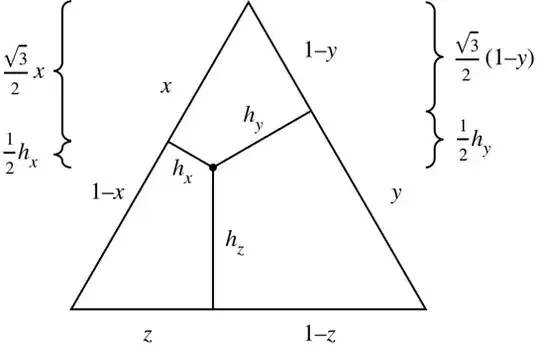
Considering the vertical distances on sides $x$ and $y$ and then repeating the same for the other side pairs: $$ \begin{align} \frac{\sqrt3}{2}x+\frac12h_x&=\frac{\sqrt3}{2}(1-y)+\frac12h_y\\ \frac{\sqrt3}{2}y+\frac12h_y&=\frac{\sqrt3}{2}(1-z)+\frac12h_z\tag{3}\\ \frac{\sqrt3}{2}z+\frac12h_z&=\frac{\sqrt3}{2}(1-x)+\frac12h_x \end{align} $$ Adding these and cancelling results in $$ x+y+z=\frac32\tag{4} $$ That is $$ |\,\overline{FA}\,|+|\,\overline{DB}\,|+|\,\overline{EC}\,|=\frac32\tag{5} $$
Thus, $(2)$ and $(5)$ yield $$ \frac{|\,\overline{FP}\,|+|\,\overline{DP}\,|+|\,\overline{EP}\,|}{|\,\overline{FA}\,|+|\,\overline{DB}\,|+|\,\overline{EC}\,|}=\frac1{\sqrt3}\tag{6} $$
It is a well-known fact (with proof sketched in the comments below the question) that $$|PD|+|PE|+|PF| = \text{height of triangle}$$ so that the numerator of the target ratio is independent of $P$. It is perhaps less-well-known that $$|AF| + |BD| + |CE| = |FB| + |DC| + |EA| = \text{semi-perimeter of triangle} \qquad (\star)$$ which effectively solves the problem.
I was unaware of this second relation, so I set about proving it by (re-)deriving a Ceva-like theorem to characterize, not concurrent lines through a triangle's vertices (aka, "cevians"), but concurrent perpendiculars to a triangle's edges (aka ... um ... "orthians"? because they're orthogonal?); the theorem says this:
Ortha's Theorem. Orthians at points $D$, $E$, $F$ on respective sides $BC$, $CA$, $AB$ of $\triangle ABC$ concur if and only if $$|AF|^2+|BD|^2+|CE|^2 = |FB|^2+|DC|^2+|EA|^2$$
Before proving this theorem, let's see how it shows $(\star)$.
Writing $s := |AB| = |BC| = |CA|$ in our equilateral triangle, we have $$|FB| = s - |AF| \qquad |DC| = s - |BD| \qquad |EA| = s - |CE|$$ Since we know the orthians at $D$, $E$, $F$ meet at $P$, we can invoke the "only if" aspect of Ortha's Theorem to conclude $$|AF|^2 + |BD|^2 + |CE|^2 = \left( s - |AF| \right)^2 + \left( s - |BD| \right)^2 + \left( s - |CE| \right)^2$$ whence $$0 = s \left( 3 s - 2 \left( |AF| + |BD| + |CE| \right)\right)$$ so that (for non-zero $s$) $$|AF|+|BD|+|CE| = \frac{3}{2}s = \text{semi-perimeter of } \triangle ABC$$
Proof of Ortha's Theorem. Orthians at points $E$ and $F$ definitely concur; call their common point $P$.
(Despite appearances in the image, $B$, $P$, and $E$ are not (necessarily) collinear; likewise $C$, $P$, $F$ ... or $A$, $P$, $D$, for that matter.)
Then ...
$$\begin{align} PD \perp BC &\iff \quad |PB|^2 - |BD|^2 = |PC|^2 - |DC|^2 &(1) \\[6pt] &\iff |PF|^2 + |FB|^2 - |BD|^2 = |PE|^2 + |CE|^2 - |DC|^2 \\ &\iff |PA|^2 - |AF|^2 + |FB|^2 - |BD|^2 = |PA|^2 - |EA|^2 + |CE|^2 - |DC|^2 \\[6pt] &\iff |AF|^2 +|BD|^2 + |CE|^2 = |FB|^2 + |DC|^2 + |EA|^2 &\square \end{align}$$
(In $(1)$, the "$\Rightarrow$" part is clear, as each side of the equation gives $|PD|^2$. The "$\Leftarrow$" part follows from slightly more effort, which is left to the reader. Note that only the "$\Rightarrow$" part needed to show $(\star)$.)
I suspect this theorem must be known in the literature. (Of course, I invented the name "Ortha" as a back-construction of my invented word "orthian", to mimic the connection between "Ceva" and "cevian".) Come to think of it, the result here is equivalent to equation $(\star\star\star)$ in this answer of mine from a few months ago that generalizes Ceva's theorem to arbitrary lines meeting a triangle. So, I guess my suspicion is that this theorem must be known somewhere else in the literature.
