Sum of areas of triangles

Question

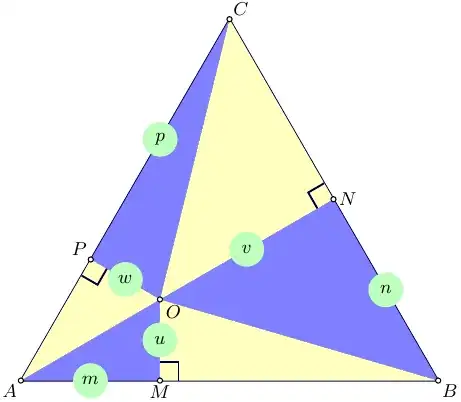
Let $ABC$ an equilateral triangle and $O$ a point in interior of $ABC$. Consider $M, N, P$ the projections on the sides $AB, BC, AC$. Then the sum of areas of triangles $ AOM, BON, COP$ is the same like the sum of areas of triangles $BOM, CON, AOP$. How to start? I try to find an elementary solution.

Well, at least it gives a relation $|AM|^2+|BN|^2+|CP|^2=|AP|^2+|BM|^2+|CN|^2$, which might help. — g.kov, Sep 08 '17 at 19:36
There is a connection with (https://math.stackexchange.com/q/651119) — Jean Marie, Sep 09 '17 at 06:19

score 2 · Accepted Answer · answered Sep 09 '17 at 13:27

Let $|AB|=|BC|=|CA|=a$, $|AM|=m$, $|BN|=n$, $|CP|=p$,

$|OM|=u$, $|ON|=v$, $|OP|=w$.

\begin{align} S_1&= S_{AMO}+S_{BNO}+S_{CPO} ,\\ S_2&= S_{AOP}+S_{BOM}+S_{CON} ,\\ S_1+S_2&=S_{ABC} . \end{align}

Given \begin{align} A&=(0,0),\quad B=(a,0),\quad C=(\tfrac12a,\tfrac{\sqrt3}2a),\\ O&=(m,u),\quad M=(m,0),\\ \end{align}

using complex arithmetics, it can be shown that \begin{align} N&=(\tfrac34a-\tfrac{\sqrt3}4\,u+\tfrac14\,m ,\ \tfrac{\sqrt3}4\,a+\tfrac34\,u-\tfrac{\sqrt3}4\,m),\\ P&=( \tfrac{\sqrt3}4\,u+\tfrac14\,m ,\ \tfrac34\,u+\tfrac{\sqrt3}4\,m),\\ S_{AMO} &= \tfrac12\,u\,m,\\ S_{BNO} &= \tfrac18\,(\sqrt3\,a-\sqrt3\,m-u)(a+\sqrt3\,u-m),\\ S_{CPO} &= \tfrac18\,(2\,a-m-\sqrt3\,u)(\sqrt3\,m-u),\\ S_1&= S_{AMO}+S_{BNO}+S_{CPO} =\tfrac{\sqrt3}8\,a^2=\tfrac12 S_{ABC} =S_2 . \end{align}

Obviously you know some excellent program to be able to do that beautiful drawing. Can you tell me which one, please? — Piquito, Sep 09 '17 at 15:57
@Piquito: Thanks for asking. Yes, this drawing was made with the Asymptote, "a powerful descriptive 2D and 3D vector graphics language that provides a natural coordinate-based framework for technical drawing. Labels and equations are typeset with LaTeX, for high-quality PostScript output." It is also included in the TeXLive distribution. — g.kov, Sep 09 '17 at 17:22

Piquito · Answer 2 · 2017-09-09T01:38:34.620

COMMENT.-You can demonstrate your problem if you are willing to "perspire" enough. The calculations are direct but tedious. I have tried, to help you, to verify the property with a numerical example, less laborious than with algebraic variables literal and would seem a counterexample because I have not found the equality of the sums. It could be that because the distances ON, OM and OP I have calculated with only a few decimal places. Anyway, here the numerical example which you could examine in more detail (if you want of course).

The equilateral triangle with vertices $A(0,0),B(4,0),C(2,2\sqrt3)$, the interior point $0=(3,1)$.

You get $$BN=1.366008053\space \space \space CP=1.634013948\\ON=0.366030053\space \space \space OP=2.098068159$$ We take the double of areas

$$\triangle AOM=3\\\triangle BON=0.500000000038016809\\\triangle COP=3.428272635660681732$$

Their sum is $$S_1=6.928272635698698541$$ $$\triangle BOM=1\\\triangle CON=0.964120211961983191\\\triangle AOP=4.964000000339318268$$ whose sum is equal to $$S_2=6.928120212301301459$$

Compare: $AOM=3$, $BON=0.5$, $COP=3.42820323027551$, $AOP=4.96410161513775$, $BOM=1$, $CON=0.964101615137755$, $S_1=6.92820323027551$, $S_2=6.92820323027551$. — g.kov, Sep 09 '17 at 11:31
Thanks you. Good your answer. Tell me about the drawing, please. — Piquito, Sep 09 '17 at 16:06

Sum of areas of triangles

2 Answers2