0

Given a triangle $\Delta ABC$. Let $A_1,B_1,C_1$ be points on the circum circle of $\Delta ABC$ such that $AA_1\parallel BC , BB_1 \parallel AC, CC_1 \parallel AB$. Through the points $A_1,B_1,C_1$ drawn lines $a_1,b_1, c_1$ which are perpendicular to lines $BC,CA,AB$ respectively. Prove that the lines $ a_1,b_1,c_1$ are concurrent

Yiorgos S. Smyrlis
  • 83,933
Cis
  • 71
  • 3
    This site works better if, instead of pretending to give us orders, you tell us where the problem comes from; why it interests you; what progress you have made on it; where you got stuck; that sort of thing. – Gerry Myerson Feb 16 '14 at 08:17
  • http://imgur.com/MKaPHPv – Shaurya Gupta Feb 16 '14 at 08:58
  • The points $A_1, B_1, C_1$ are the reflections of the points $A, B, C$ in the respective perpendicular bisectors of the sides $BC, CA, AB$. Hence, the lines $a_1, b_1, c_1$ are the reflections of the altitudes of triangle $ABC$ in the respective perpendicular bisectors of the sides $BC, CA, AB$. Thus, they intersect at the reflection of the orthocenter through the circumcenter. – darij grinberg Sep 29 '18 at 03:25

1 Answers1

1

I'll use slightly different notation... with $A^\prime$ for $A_1$, etc. I'll also refer to what I introduced (and proved) as "Ortha's Theorem" in this answer.

Ortha's Theorem. Orthians* at points $D$, $E$, $F$ on respective sides $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ concur if and only if $$|\overline{BD}|^2 + |\overline{CE}|^2 + |\overline{AF}|^2 = |\overline{DC}|^2 + |\overline{EA}|^2 + |\overline{FB}|^2 \qquad (\star)$$

*An "orthian" is a line perpendicular to the side of a triangle at a given point.

Let $D$, $E$, $F$, $D^\prime$, $E^\prime$, $F^\prime$ be the feet of perpendiculars from $A$, $B$, $C$, $A^\prime$, $B^\prime$, $C^\prime$ to the sides of $\triangle ABC$ as shown.

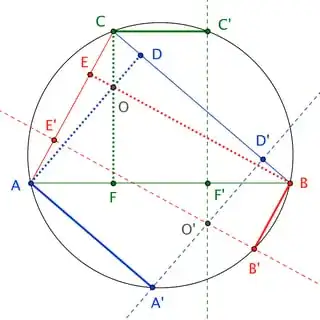
enter image description here

Observe that, since $\overline{AB}$ and $\overline{CC^\prime}$ (as parallel chords of the circumcircle) are bases of an isosceles trapezoid, we must have

$$|\overline{BD^\prime}| = |\overline{DC}| \qquad \text{and} \qquad |\overline{D^\prime C}| = |\overline{BD}|$$

Likewise,

$$|\overline{CE^\prime}| = |\overline{EA}| \qquad |\overline{E^\prime A}| = |\overline{CE}| \qquad |\overline{AF^\prime}| = |\overline{FB}| \qquad |\overline{F^\prime B}| = |\overline{AF}|$$

Therefore, by Ortha's Theorem, orthians $\overleftrightarrow{AD}$, $\overleftrightarrow{BE}$, $\overleftrightarrow{CF}$ concur if and only if orthians $\overleftrightarrow{AD^\prime}$, $\overleftrightarrow{BE^\prime}$, $\overleftrightarrow{CF^\prime}$ concur (since $(\star)$ holds in both cases, or in neither). It is well-known that the former trio (as altitudes of $\triangle ABC$) concur at the triangle's orthocenter, $O$; thus, the latter trio concur, as well. $\square$

Community
  • 1
Blue
  • 75,673