Describing a Wave

Question

I have this wave in front of me, and I am to describe this into a math description such as its function that is equivalent to representing this wave. I have no idea how to start and could use some detailed guidance if possible, or just how to go about getting an expression for it, as well as finding the amplitude, phase, ... etc.

The picture of the waveform is below:

Answer 1

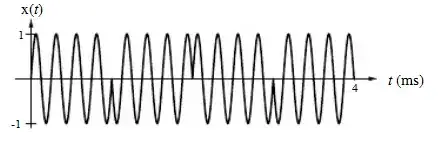
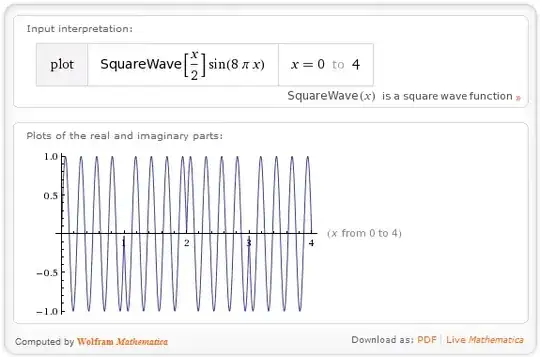
$$-\sin\left(8\pi\left|x-2\left\lfloor\frac{x}{2}\right\rfloor-1\right|\right)$$ seems to work...

---

How to make your own periodic function

Questions like this or this keep turning up here, so for completeness, I'm documenting a recipe for constructing periodic functions.

The first thing you need to do is to figure out your "repeating unit"; that is, you should have some function $f(x)$ defined over some interval $[a,b]$ as a starting point, such that the final function is a periodically extended version for $x$ outside the interval $[a,b]$. (I will be assuming for the rest of this answer that $f(a)=f(b)$; otherwise, as with this answer, some care and finesse is required if the behavior at the function's jump discontinuities matters to you.)

The key ingredient for making your custom periodic function is the sawtooth, i.e. the function $x-\lfloor x\rfloor $. This has the property that it is equal to $x$ in the interval $[0,1)$, and repeats thereafter.

From this, the basic sawtooth can be rescaled and translated like so:

$$x-(b-a)\left\lfloor\frac{x-a}{b-a}\right\rfloor$$

This function now has the property of being equal to $x$ within the interval $[a,b)$, and repeats thereafter. Thus, if you want your function to be a repeated version of the function $f(x)$ over the interval $[a,b]$, and $f(a)=f(b)$,

$$f\left(x-(b-a)\left\lfloor\frac{x-a}{b-a}\right\rfloor\right)$$

is the desired periodic function.

Alternatively, since

$$x\bmod y=x-y\left\lfloor\frac{x}{y}\right\rfloor$$

the modulo function can also be used to represent the sawtooth.

(For some purposes, one might need to multiply the periodic function thus obtained with an appropriate square wave factor like in Zev's answer to the semicircle question, but I shan't be considering that filigree here.)

---

Going back to the OP's problem, consider the function $-\sin(8\pi |x|)$ (alternatively, $-\mathrm{sign}(x)\sin(8\pi x)$):

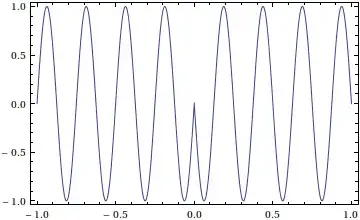
This looks very much like one period of the OP's required function, except that it is defined over the interval $[-1,1]$ and not over $[0,2]$. A translation fixes that: $-\sin(8\pi |x-1|)$. One now replaces the $x$ with a sawtooth over $[0,2)$ like so:

$$-\sin\left(8\pi\left|\left(x-(2-0)\left\lfloor\frac{x-0}{2-0}\right\rfloor\right)-1\right|\right)$$

and simplifying that yields the function I gave earlier.

Answer 2

It looks like 4 sine wavelengths, then another 4 upside down, 4 more right side up, and then 4 upside down, all scrunched up into the interval $[0,4]$. It repeats every interval of length $2$, so that's the period, and the amplitude can be seen from the graph as $1$. First what we'll do is dilate $\sin$ to accommodate 4 full wavelengths in $[0,1]$: this is simply $\sin(8\pi x)$ (this follows because $2\pi$ divided by $1/4$ is $8\pi$). Then we'll multiply this by a function which is $+1$ on $[0,1)$, $-1$ on $[1,2)$ and so forth: this is just the square wave stretched by a factor of 2, or $S(t/2)$. Hence the function is $$x(t)=\sin(8\pi t)S(t/2).$$

Wolfram Alpha shows this is correct:

Answer 3

So the phase looks like increasing and then reversing its direction and decreasing in the same manner. So phase change looks like a "triangle wave". According to this, I think you can write it as $$ \sin( \arcsin( \sin (x))) $$ I am not sure about the triangle wave formula, wiki has something different but you can correct it yourself.

EDIT : I think this link is better than the previous one.

EDIT2 : It doesn't work, see Anon's answer.