@Haris Gusic : I have seen your solution which fits nicely the objectives of the asker with its different tunable parameters.
I propose here two alternatives, an intuitive one, using linear algebra, and another one more 'numerical analysis' oriented.
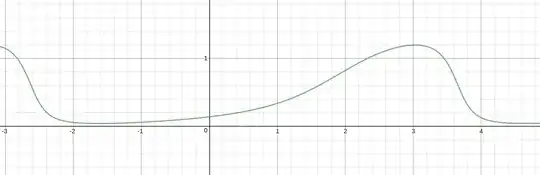
1) I have been striken by the fact that the curve desired by Aybe can be considered as a perspective view (or shadow) of a sine curve (or a power of a sine curve) : see Fig. 1 displaying the (red) curve of $y=\sin(x)^n$ and its (blue) perspective image, with parametric equations given by
$$\begin{cases}x&=&t+a\sin(t)^n\\y&=&b\sin(t)^n\end{cases} \ \ \text{here, with } \ \begin{cases}n&=&4\\a&=&0.8\\b&=&0.1\end{cases}$$

Fig. 1. The blue curve as a "shadow" of the red curve.
Why that ? This "shadow effect" is rendered by a so-called horizontal "shear mapping" (https://en.wikipedia.org/wiki/Shear_mapping) or "transvection", a linear operation with an upper triangular matrix:
$$\color{blue}{\binom{x}{y}}=\begin{pmatrix}1&a\\0&b\end{pmatrix}\color{red}{\binom{t}{\sin(t)^n}}$$
(The first column of this matrix reflects the fact that the horizontal direction is preserved whereas the second column with $a,b>0$ gives to the former vertical direction a certain leaning to the right).
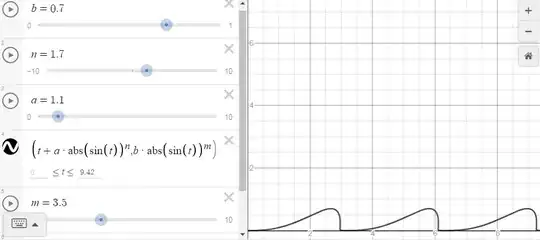
Fig. 2 : Graphical representation using Desmos. Please note that $\sin$ function has been placed between absolute value signs in order to allow non-integer exponents. A supplementary parameter $m$ has also been introduced. This is a very tunable solution : one can even, in this way, obtain breaking waves...
2) A "numerical analysis" method using quadratic splines.
I will not enter into the details because it is not sure at all that you are acquainted with such curves, which are made of arcs of parabolas connected in a "smooth" way (https://wordsandbuttons.online/quadric_splines_are_useful_too.html).

Fig. 3 : A quadratic spline solution based on 3 parabolas (red, magenta, blue) connected in a smooth way, repeated "ad libidum".
Here is the Matlab program that has generated Figure 3 (please note the three plotting operations for the red, magenta and blue parabolas with right translation variable $k$) :
clear all;close all;hold on;
t=0:0.01:1;
for k=0:6:18
plot(t.^2 + 2*t+k, t.^2,'r');
plot(-2*t.^2+4*t+3+k,-2*t.^2+2*t+1,'m');
plot(t.^2+5+k,(1-t).^2,'b');
end;
If you want to do the same with Desmos, here is a way to do it (it can be very instructive to enlarge a little the domain of parameter $t$ by taking for example $-0.5 \leq t \leq 1.5$ in order to understand what are these parabolas):
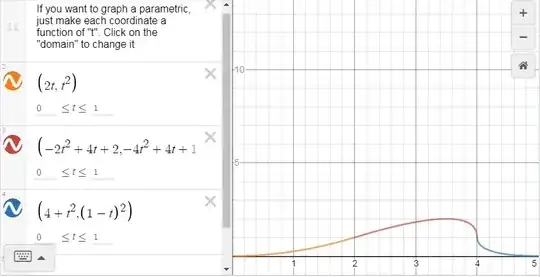
Fig. 4.