I am looking for a closed-form formula for something like this:
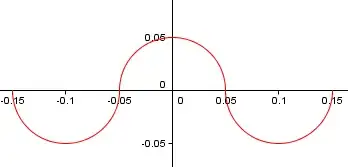
Can anybody help - Thank you!
Asked
Active
Viewed 2,501 times
5
-
And I'm assuming you don't want the closed form in terms of a piecewise definition. – jspecter Jun 09 '11 at 14:51
-
Have you tried to use the Fourier transform? Or would you object to the resulting infinite sums? – t.b. Jun 09 '11 at 14:59
-
@jspecter: No, please no piecewise def. @Theo: Infinite sums are ok, I think even necessary for the nearly perpendicular inflection points (=infinite slope). – vonjd Jun 09 '11 at 15:04
-
Almost: $\sqrt{1 - \bigg(\frac{2}{\pi}\sin^{-1}\Big(\cos\big(\frac{\pi}{2}x\big)\Big)\bigg)^2}$, WolframAlpha plot – Jun 09 '11 at 15:12
-
I now remember that I stumbled upon this phenomenon when you iterate trig funcs: http://www.wolframalpha.com/input/?i=plot+sin%28sin%28sin%28sin%28sin%28sin%28sin%28sin%28x%29%29%29%29%29%29%29%29 - perhaps this helps and can be combined with some of the other ideas here?!? – vonjd Jun 09 '11 at 15:18
-
1Just curious: Why do you want to avoid a piecewise definition? – JT_NL Aug 07 '11 at 13:43
-
A related question. P.S. I edited a bit so that the keyword "semicircle" turns up; this question cannot be seen when the search term "semicircle" is used. I left the linked question to use "half-circles" instead. – J. M. ain't a mathematician Aug 07 '11 at 18:11
3 Answers
7
This works (for circles of radius $r$):
$$f(x)=(-1)^{\displaystyle\left\lfloor \frac{x}{2r}+\frac{1}{2}\right\rfloor}\sqrt{r^2-\left(x-2r\left\lfloor\frac{x}{2r}+\frac{1}{2}\right\rfloor\right)^2}$$
Image for $r=1$:
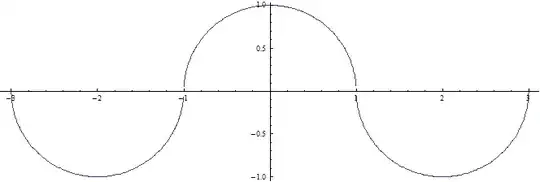
Mathematica code:
r = 1; Plot[(-1)^Floor[x/(2r) + 0.5] Sqrt[r^2 - (x - (2r)Floor[x/(2r) + 0.5])^2],
{x, -3, 3}, AspectRatio -> 1/3]
Zev Chonoles
- 129,973
-
@Zev: I don't know how to fix this, but I think it goes into the right direction. Floor func is ok. – vonjd Jun 09 '11 at 15:15
-
WA-plot: http://www.wolframalpha.com/input/?i=Plot+%28-1%29^%28Floor%5B%28x%2F2+%2B+0.5%29%5D%29+Sqrt%5B1+-+%28x+-+2+Floor%5Bx%2F2+%2B+0.5%5D%29^2%5D - How did you find it? – vonjd Jun 09 '11 at 15:24
-
@vonjd: I figured we needed a $(-1)^{\text{something}}$ to get the flipping about the $x$-axis, figured out what the something was based on the period we needed, and then used the subtracting-the-floor-function trick to shift each segment $[r(2n-1),r(2n+1)]$ of the $x$-axis down to the $[-r,r]$ segment, then used the formula for the (upper half of a) circle on the segment $[-r,r]$. – Zev Chonoles Jun 09 '11 at 15:28
-
(in general, $a\lfloor\frac{b}{a}\rfloor$ is the largest multiple of $a$ less than $b$, so subtracting it from $b$ gives the "remainder") – Zev Chonoles Jun 09 '11 at 15:30
-
Zev: If you use four blank spaces as indentation instead of the
>then you get acodeblock, which makes your code a bit easier to read because a monospace font is used. (you need to do the line breaks manually to avoid a scroll bar) – t.b. Jun 09 '11 at 15:32 -
-
@ZevChonoles +1. Good function for moving spacecrafts in computer games. – MathNerd Sep 20 '14 at 16:25
2
I have come up with an equation, which can be found at this desmos calculator I made. I derived this equation from $\arcsin(\sin(x))$ giving a zig-zag, and $\sqrt{-x^2+1}$ giving semicircles, then multiplied by the sign of cosine wave to invert every other semicircle. $n$ is the horizontal shift, $r$ is the radius.
the full form of the equation is as follows, with $n$ being the horizontal shift, and $r$ being the radius: $$f\left(x\right)=r\sqrt{-\left(\frac{2\arcsin\left(\sin\left(\frac{\pi x}{2r}+n\pi\right)\right)}{\pi}\right)^{2}+1}\cdot\operatorname{sign}\left(\cos\left(\frac{\pi x}{2r}+n\pi\right)\right)$$
torzod
- 21
- 3
1
a good approximation is
y = |sin x|^(sin x) + 11/7 sin x
here is my research. I took a sine wave and circles and plotted the difference in their y values then made an equation that roughly matched it, then added sin x to that.
