5

I'm trying to show different convergents, and this is the first one i'm having problems with.

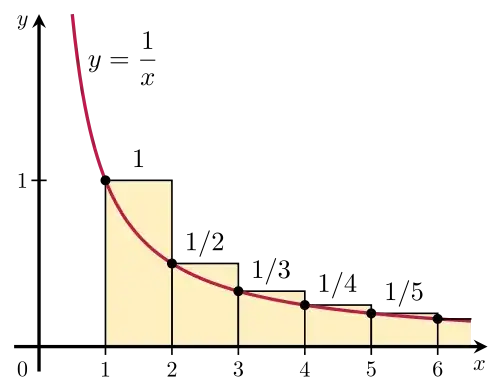
$\dfrac11 + \dfrac 12 + \ldots + \dfrac 1n - \log n \rightarrow \gamma$ Like it's the definition of euler's constant, but how to show that this expression is convergent( i don't mean convergent to specific number, just convergent ).

I tried d'alambert's criterion. This is : if $$\left| \frac{a_{n+1}}{a_{n}}\right | < 1$$ then $a_{n}$ is convergent.

But i end up with something like

$$\frac{H_{n} + (n+1) - ln(n+1)}{H_{n} - \ln(n)}$$ where $H_{n}$ is n-th harmonic number. I have no clue how to work on it further.

Would love to get some hints or solutions on this.

Cheers

Thomas Andrews
  • 177,126
Krzysztof Lewko
  • 2,312

3 Answers3

6

$\gamma$ is the limit of the sum of the slightly bigger than triangle pieces of this diagram (from Wikipedia)

enter image description here

As $n$ increases, the sum increases, but clearly has an upper bound of $1$ and therefore converges to a limit $\gamma$ less than or equal to $1$.

This picture also makes it obvious why $\gamma$ is slightly more than $0.5$

In fact the partial sum of the pieces is $H(n)-\log_e(n+1)$ but the difference $\log_e(n+1) - \log_e(n)$ is $O(\frac1n)$, so does not affect the convergence to $\gamma$.

Henry
  • 157,058
3

Let $$u_n=\sum_{k=1}^n\frac 1 k-\log n$$ then $$u_{n}-u_{n-1}=\frac{1}{n}+\log\left(1-\frac 1 n\right)\sim_\infty-\frac{1}{2n^2}$$ so the series $\displaystyle\sum_{n\ge2}u_{n}-u_{n-1}$ is convergent by asymptotic comparison and then the sequence $(u_n)_n$ is convergent by telescoping.

  • 1
    Well, about what asymptotic comparison are you talking about? I was taught that asymptotic is anbn for some bn constructed from an. And as this fraction goes to some limit we can say it's convergent. But here you used subtraction and i'm not sure what happened here. Thanks. – Krzysztof Lewko Dec 15 '13 at 11:02
1

the sequence $U_n$is strictly decreasing sequence. as, $U_{n+1}-U_n=\frac{1}{n+1}-\log (1+\frac{1}{n})<0$;which can be checked by Riemann's integral on the function $f(x)=\frac{1}{x}$. now again using Riemann's integral we can show, $\frac{1}{n}>\log(n+1)-\log(n)$,so, $$\sum_{k=1}^{n}\frac{1}{k}>(\log 2-\log 1)+(\log 3-\log 2)+(\log 4-\log 3)+....+(\log(n+1)-\log n )=\log(1+n)$$ $$U_n>\log(1+n)-\log n>0;$$ so,$U_n$ has a lower bound as well as decreasing,hence $U_n$ converges.

Mariana
  • 1,253
sapta
  • 91