Why $\,\gcd(a,b) = \gcd(b,a\bmod b)$? [understanding Euclidean algorithm]

Question

I am not understanding how the following formular works

http://en.wikipedia.org/wiki/Greatest_common_divisor#Using_Euclid.27s_algorithm

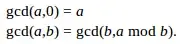
Actually what I did (for my programming homework was loop through the max of 2 numbers until I get 1 that divides both given numbers without a remainder). Bruteforce, so not ideal. So I want to understand more about this formular instead of just using it.

public static int gcd(int a, int b) {
  /**
   * Get max of both numbers
   * Loop down max number and test if its divisible by both numbers
   * if yes, thats the answer, else continue
   * if no answer, return 0
   */
  int max = Math.max(a, b);
  for (int i = max; i > 0; i--) {
    if (a % i == 0 && b % i ==0) {
      return i;
    }
  }
  return 0;
}

Answer 1

The basic idea is this: if you want gcd($a$, $b$) and $a>b$, then we can instead compute gcd($b, a \bmod b$) and we've made progress. It's progress because when $a>b$, we know $a \bmod b$ is smaller than $b$, it's a remainder after all. And if we make positive inputs smaller and smaller, eventually we must terminate.

The real question is this: why is gcd($a$, $b$) the same as gcd($b, a \bmod b$)?

Well, let's answer an easier question. Instead of trying to wrap your head around $a \bmod b$, let's restate the problem. Why is gcd($a$, $b$) the same as gcd($b, a-b$)? This question is almost the same, but we're using minus instead of mod because it's easier to understand when this stuff is new to you. And mod is just a repeated application of minus anyway, right?

So let's prove the "easier" version. Well, if some divisor $d$ goes evenly into $a$ and $b$, then it must go into their difference $a-b$, right? To be more mathematical, if $a = kd$ and $b=jd$, then $a-b = kd-jd = (k-j)d$ and clearly $d$ goes evenly into $(k-j)d$. Also, if $d$ goes evenly into $(a-b)$ then any $d$ dividing $a$ must divide $b$, so we're done.

If this still isn't clear, draw a number line and convince yourself that two multiples of 3 (for example) are always a multiple of 3 apart. Then convince yourself that any multiple of 3 plus a multiple of 3 must also be a multiple of 3.

Then try it for numbers other than 3.

Answer 2

$a{\rm\ mod\ }b$ is the remainder when you divide $a$ by $b$, so we can say two things about it: it is $a-bq$ for some integer $q$, and it is between $0$ and $b-1$, inclusive.

I want to show $\gcd(a,b)=\gcd(b,a{\rm\ mod\ }b)$.

Let $d=\gcd(a,b)$. Then $d$ divides both $a$ and $b$. So it divides both $a-bq$ and $b$. So it divides $\gcd(b,a{\rm\ mod\ }b)$.

Conversely, let $e=\gcd(b,a{\rm\ mod\ }b)$. Then $e$ divides both $b$ and $a-bq$. So it divides both $a$ and $b$. so it divides $\gcd(a,b)$, and we are done.

Now the only question remaining about the formula is why it always gives an answer, that is, why it can't just keep going forever. Well, supposing $a\gt b$, and comparing $\gcd(a,b)$ and $\gcd(b,a{\rm\ mod\ }b)$, we've decreased both arguments (that is, replacing $a$ with $b$, and replacing $b$ with $a{\rm\ mod\ }b$, we've replaced both with things that are smaller). The way the (positive) integers work, that can't go on forever. It has to stop sometime. But the only way it can stop is when $b=0$ (since if $b\gt0$ you can always keep going), and then $\gcd(a,0)=a$ kicks in.

Answer 3

If $\rm\:d\:|\:b\:$ then $\rm\:d\:|\:a \iff d\ |\ a-nb.\,$ Thus $\rm\ a,b\ $ and $\rm\ a-nb,\,b\ $ have the same common divisors, therefore the same greatest common divisor. Finally $\rm\ a\ mod\ b\, = \, a-nb\ $ for some $\rm\:n\in \mathbb Z.$

Answer 4

It all rests on one simple fact. If $b = aq + r$ and $b, q, a, r\in \mathbb{Z}$, then $\gcd(a,b) = \gcd(a,r)$. Just show that an integer divides $a$ and $b$ iff it divides $a$ and $r$ and you are done.

Answer 5

Lemma : If $c$ divides both $a$ and $b$ then $c$ divides $gcd(a,b)$, i.e.,

$c|a$ and $c|b\implies c|gcd(a,b)$

We have to prove $gcd(a,b)=gcd(a,a \mod b )$

where $k>0$ and $k\in \mathbb{Z}_+$.

• Part 1

Let $d_1=gcd(a,b)$ then $d_1|a$ and $d_1|b$ $$ \implies a=t_1d_1\quad\&\quad b=t_2d_1\\ \implies a=t_1d_1\quad\&\quad kb=kt_2d_1=t_3d_1\\ \implies r=a\mod b=a-kb=(t_1-t_3)d_1=t_4d_1\\ i.e., d_1|b\quad\&\quad d_1|a\mod b $$ Using Lemma we can conclude that $d_1|gcd(b,a\mod b)=d_2$

• Part 2

$d_2=gcd(b,a\mod b)\implies d_2|b\quad\&\quad d_2|a\mod b$ $$ \implies d_2|b\quad\&\quad d_2|a-kb\\ \implies d_2|kb\quad\&\quad d_2|a-kb\\ \implies d_2|kb+(a-kb)\implies d_2|a\\ \text{Using Lemma implies, }d_2|b\quad\&\quad d_2|a \implies d_2|gcd(a,b)=d_1 $$

Therefore, $gcd(b,a\mod b)|gcd(a,b)$ and $gcd(a,b)|gcd(b,a\mod b)$ implies $gcd(a,b)=gcd(b,a\mod b)$