What is the exact and precise definition of an ANGLE?

Question

On wikipedea I found a definition of an Angle as such:

"In order to measure an angle θ, a circular arc centered at the vertex of the angle is drawn, e.g. with a pair of compasses. The length of the arc s is then divided by the radius of the arc r, and possibly multiplied by a scaling constant $k$ (which depends on the units of measurement that are chosen): $$\theta = k \frac{s}{r}.$$ The value of θ thus defined is independent of the size of the circle: if the length of the radius is changed then the arc length changes in the same proportion, so the ratio $s/r$ is unaltered.'

And the definition of circular arc is given as:

"a circular arc is a segment of a circle, or of its circumference (boundary) if the circle is considered to be a disc."

Now since circular arc is a segment of a circle we are not supposed to have circular arc of length more than circumference of the circle. So we cannot define angles more than $2\pi$ in this manner. But I found a topic in the book, "Unified algebra and trigonometry" (Addison-Wesley mathematics series) art 3-5. I've posted it as an answer to the question

https://physics.stackexchange.com/questions/87057/angular-displacement/87066#87066.

There the author of the book explains that we can have circular arc more than the circumference of a circle as:
"....where the circular arc $\stackrel \frown {PP}^{′}$ denoted by $s$,.... since the number of revolutions of any angle is determined by the ratio of the intercepted circular arc length $s$ to circumference of the circle we define, magnitude of an angle in revolutions as

Angle in revolutions$ = s/2πr$..."

means there can be angles of more than $2\pi$ .

Question1:Does the definition of an angle depends upon its use in physics?

Question2: if we assign a point on a solid body named $P$ having an initial angle $\theta$ after this solid body rotates a full circle can we assume the angle of point $P$ after the revolution to be again $\theta$ or $\theta +2\pi$. Please state a precise definition to support the validity of this argument.

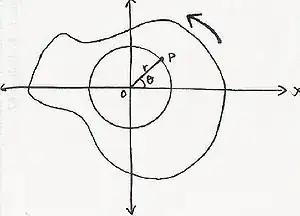As I understands if we assign polar-coordinates to point $P$ these polar coordinates will be $(\pm r,\theta\pm 2n\pi)$ and but if rotation is involved should we consider the angle used as "oriented" or "non-oriented".

Answer 1

"Angle" is a touchy subject. There are (at least) the following three interpretations, applicable depending on circumstances.

(a) The simplest is the following: Given two nonzero vectors ${\bf x}$, ${\bf y}\in{\mathbb R}^n$, $\>n\geq2$, the (nonoriented) angle $\alpha$ between them is the nonnegative number $$\alpha:=\arccos{{\bf x}\cdot{\bf y}\over|{\bf x}|\>|{\bf y}|}\in[0,\pi]\ .$$ In particular: Given two rays emanating from the same point $P$ in space the "enclosed angle $\alpha$" is a number between $0$ and $\pi$ inclusive, and is equal to the length of the shorter arc cut out on the unit circle in the plane of these two rays.

This idea of angle is also at the basis of spherical trigonometry, where the angle between two points ${\bf u}$, ${\bf v}\in S^2$ is considered as distance between these two points. As such it satisfies the triangle inequality.

(b) When some rotation about the origin in ${\mathbb R}^2$ is involved then the group $SO(2)$ steps into action, and it makes sense to talk about oriented angles. An oriented angle is an equivalence class of real numbers modulo $2\pi$. Each such class has a unique representant in the interval $[0,2\pi[\ $, or in the interval $\ ]{-\pi},\pi]$, and the set of these classes is bijectively related to $SO(2)$.

An example: The map $$T:\quad (x,y)\mapsto(x\cos\alpha-y\sin\alpha,\ x\sin\alpha+y\cos\alpha)$$ is a rotation of the euclidean plane about the angle $\alpha\in{\mathbb R}/(2\pi{\mathbb Z})$. When the rotation is physically performed in time and all points are in fact rotated carousel-like $n$ full turns before stopping at the right place the information about $n$ is not present in $T$.

(c) The circle group $SO(2)$ has the full real line ${\mathbb R}$ as its "universal cover". Sometimes it is desirable to work in ${\mathbb R}$ when talking about angles, e.g., when studying the logarithmic spiral $$\sigma:\quad t\mapsto (e^t\cos t,e^t\sin t)\qquad(-\infty<t<\infty)\ .$$

Another important example is the following: You have a closed curve $$\gamma:\quad t\mapsto {\bf z}(t)=\bigl(x(t),y(t)\bigr)\in\dot{\mathbb R}^2\qquad(0\leq t\leq L)$$ which encircles the origin a certain number $n$ of times. In order to compute this $n$ we cumulate the infinitesimal changes of $\phi(t):=\arg\>{\bf z}(t)$ and in the end divide by $2\pi$. Here $\phi(t)$ is only "defined up to $2\pi$", as in (b), but $\phi'(t)$ is well defined, and is given by $$\phi'(t)={x(t)y'(t)-x'(t)y(t)\over x^2(t)+y^2(t)}\qquad(0\leq t\leq L)\ .$$ It follows that the total argument increase $\Delta\phi\in{\mathbb R}$ along $\gamma$ is given by $$\Delta\phi=\int_0^L\phi'(t)\ dt=\int_0^L {x(t)y'(t)-x'(t)y(t)\over x^2(t)+y^2(t)}\ dt\ ,$$ from which we then obtain $n={\Delta\phi\over 2\pi}$. In complex analysis this number appears as $$n(\gamma,0)={1\over2\pi i}\int\nolimits_\gamma{dz\over z}\ .$$

Answer 2

I'm not sure if defining angle in terms of cosine/sine makes sense if you define cosine/sine in terms of angle in the first place (eg. the so-called "cosine of an angle"...).

The best definition I have so far is:

Definition (angle).
The angle between 2 vectors $a,b \in \mathbb{R}^n$ is the "normalized", scale-independent, dimensionless arclength "connecting " $a$ and $b$ on any circle that is coplanar to both $a$ and $b$.

Slightly more precisely:

Definition (angle).
Let $a,b$ be a vectors in $\mathbb{R}^n$.
Let $C_r \subseteq \mathbb{R}^n$ be a circle of radius $r \in \mathbb{R}^+$ that is coplanar to both $a$ and $b$ and is centered at the origin of $\mathbb{R}^n$.
Let $\ell \in [0..\pi]$ be the arclength of the shortest circular arc on $C_r$ that "connects" $a$ and $b$.
Now the angle between vectors $a$ and $b$ is ${\ell \over r}$.

Here is (what should be) an equivalent definition:

Definition (angle).
Let $a,b$ be a vectors in $\mathbb{R^n}$.
The angle between $a$ and $b$ is the arclength of the (shortest) circular arc that that lies on the (unique) unit circle that is coplanar to both $a$ and $b$.
(To turn this arclength into a dimensionless number, I think you just divide by the radius, which is 1.)

Slightly more, err, "formally":

"Lemma" (existence of coplanar circles).
Let $a,b$ be a vectors in $\mathbb{R^n}$.
Let $C_r \subseteq \mathbb{R}^n$ be a circle of radius $r \in \mathbb{R}^+$ centered at the origin of $\mathbb{R}^n$.
Now there exists an infinite family $\{C_r | r \in \mathbb{R}^+\}$ of coplanar nontrivial circles parameterized by $\mathbb{R}^+$ centered at the origin of $\mathbb{R}^n$ that are also coplanar to the vectors $a$ and $b$.
Proof. I don't know.
Note. A nontrivial circle is a circle of nonzero radius.
Note. Coplanar means they lie in the same plane.

Definition (angle).
Let $a,b$ be a vectors in $\mathbb{R^n}$.
Let $C_r \in \{C_r | r \in \mathbb{R}^+\}$, where $\{C_r | r \in \mathbb{R}^+\}$ is as in the Lemma above, whose existence is guaranteed by the same.
Let $\ell \in [0..\pi]$ be the arclength of the shortest circular arc on $C_r$ that "connects" $a$ and $b$.
Now the angle between vectors $a$ and $b$ is ${\ell \over r}$.
Note. This definition only makes sense if it's even possible to define circle, circular arc and arclength of a circular arc without using the notion of angle.

In short: the angle is just the arclength normalized by the radius.

• I think it's possible to generalize this to higher dimensional angles, eg. steradians, by replacing arclengths on the unit circle with spherical caps on the unit sphere.
• I think an analogous arclength definition may also apply to hyperbolic angle.