How closely can we estimate $\sum_{i=0}^n \sqrt{i}$

Question

By looking at an integral and bounding the error?

Answer 1

This was an interesting challenge, to try and come up with an estimate for this sum in an elementary way.

The estimate I got was

$$1 + \sqrt{2} + \dots + \sqrt{n} \sim \frac{2}{3}n^{3/2} + \frac{\sqrt{n}}{2} + C$$

for some constant $C$ which appears to be close to $-0.207$ (which I guess will be $\zeta(-1/2)$).

(By $a_{n} \sim b_{n}$ I mean $\lim_{n \rightarrow \infty} (a_{n}-b_{n}) = 0$)

I believe here is a completely elementary proof of that fact:

First consider the inequality for $x > 0$ and $k > 0$.

$$ \sqrt{x} \le \frac{x}{2\sqrt{k}} + \frac{\sqrt{k}}{2}$$

This follows easily by the arithmetic mean $\ge$ geometric mean inequality.

Thus we have that

$$\int_{k}^{k+1} \sqrt{x} \ dx \le \int_{k}^{k+1} (\frac{x}{2\sqrt{k}} + \frac{\sqrt{k}}{2}) \ dx$$

$$ = \frac{(k+1)^2 - k^2}{4\sqrt{k}} + \frac{\sqrt{k}}{2} = \sqrt{k} + \frac{1}{4\sqrt{k}}$$

Thus $$\sum_{k=1}^{n-1} \int_{k}^{k+1} \sqrt{x} \ dx \le \sum_{k=1}^{n-1} (\sqrt{k} + \frac{1}{4\sqrt{k}})$$

i.e.

$$\int_{1}^{n} \sqrt{x} \ dx \le \sum_{k=1}^{n-1} (\sqrt{k} + \frac{1}{4\sqrt{k}})$$

and so

$$ \frac{2}{3} n^{3/2} - \frac{2}{3} \le \sum_{k=1}^{n-1} (\sqrt{k} + \frac{1}{4\sqrt{k}})$$

Now we have inequality

$$\frac{1}{2\sqrt{k}} < \frac{1}{\sqrt{k} + \sqrt{k-1}} = \sqrt{k} -\sqrt{k-1}$$

And so, we have that

$$ \sum_{k=1}^{n-1} \frac{1}{4\sqrt{k}} < \frac{\sqrt{n-1}}{2}$$

Thus,

$$ \frac{2}{3} n^{3/2} - \frac{2}{3} \le \frac{\sqrt{n-1}}{2} + \sum_{k=1}^{n-1} \sqrt{k} $$

So if $$S_{n} = \sum_{k=1}^{n} \sqrt{k}$$ we have that

$$S_{n} \ge \frac{2}{3} n^{3/2} - \frac{2}{3} + \sqrt{n} - \frac{\sqrt{n-1}}{2} \ge \frac{2}{3} n^{3/2} - \frac{2}{3} + \frac{\sqrt{n}}{2}$$

Now let $$G_{n} = S_{n} - \frac{2}{3} n^{3/2} - \frac{\sqrt{n}}{2}$$

We have that $$G_{n} \ge -\frac{2}{3}$$

We can easily show that (using tedious but not too complicated algebra^*) $$G_{n+1} < G_{n}$$ and so $G_{n}$ is a convergent sequence, as it is bounded below and monotonically decreasing.

Thus there exists a constant $C$ (the limit of $G_{n}$) such that

$$1 + \sqrt{2} + \dots + \sqrt{n} \sim \frac{2}{3}n^{3/2} + \frac{\sqrt{n}}{2} + C$$

---

^* For the sake of completeness, we show that $G_{n+1} < G_{n}$.

Consider $$6(G_{n}-G_{n+1}) = 4(n+1)\sqrt{n+1} + 3\sqrt{n+1} - 6\sqrt{n+1} - 4n\sqrt{n} - 3\sqrt{n}$$ $$ = \sqrt{n+1} + 4n(\sqrt{n+1} -\sqrt{n}) - 3\sqrt{n}$$

Multiplying by $\sqrt{n+1} + \sqrt{n}$ does not change the sign, so we look at

$$ \sqrt{n+1}(\sqrt{n+1} + \sqrt{n}) + 4n - 3\sqrt{n}(\sqrt{n+1} + \sqrt{n})$$ $$ = 2n+1 - 2\sqrt{n^2 + n}$$

Now $$ (2n+1)^2 = 4n^2 + 4n + 1 > 4n^2 + 4n = (2\sqrt{n^2+n}) ^2$$

Hence

$$ 2n+1 > 2\sqrt{n^2+n}$$

and so

$$G_{n} > G_{n+1}$$

Answer 2

In case you were wondering, like me, Moron's excellent proof adapts easily to show that

$$1 + \sqrt[3]{2} + \dots + \sqrt[3]{n} \sim \frac{3}{4}n^{4/3} + \frac{\sqrt[3]{n}}{2} + C,$$

for some constant $C.$ In this case $C = \zeta(-1/3) \approx -0.277343.$

Where, as before, $a_n \sim b_n$ means $\lim_{n \rightarrow \infty} (a_{n}-b_{n}) = 0.$

Similar to the previous proof, we use the AM-GM inequality to show

$$\sqrt[3]{x} \le \frac{x}{3k^{2/3}} + \frac{2k^{1/3}}{3}.$$

Summing from $k=1$ to $n-1$ and integrating we arrive at $$ \frac{3}{4}n^{4/3} - \frac{3}{4} \le \sum_{k=1}^{n-1}\sqrt[3]{n} + \frac{1}{6}\sum_{k=1}^{n-1} \frac{1}{k^{2/3}}, \qquad n>1.$$ And so, $$\sum_{k=1}^{n}\sqrt[3]{n} \ge \frac{3}{4}n^{4/3} + n^{1/3} - \frac{3}{4} - \frac{1}{6}\sum_{k=1}^{n-1} \frac{1}{k^{2/3}}, \qquad n>1.$$

Using $\sum_{k=1}^{n-1} \frac{1}{k^{2/3}} \le 1+ \int_1^n x^{-2/3} dx, \qquad n>1,$ we obtain

$$\frac{1}{6}\sum_{k=1}^{n-1} \frac{1}{k^{2/3}} \le \frac{1}{2}n^{1/3} - \frac{1}{3}.$$

And hence $$\sum_{k=1}^{n}\sqrt[3]{n} \ge \frac{3}{4}n^{4/3} + \frac{1}{2}n^{1/3} - \frac{5}{12}, \qquad n>1.$$

As in the previous argument, set

$$G_n = \sum_{k=1}^{n}\sqrt[3]{n} - \frac{3}{4}n^{4/3} - \frac{1}{2}n^{1/3}.$$

Then $G_n \ge -5/12,$ and we can show $G_n – G_{n+1} > 0$ by showing that $$\frac{(n+1)^{4/3} – n^{4/3}}{(n+1)^{1/3} + n^{1/3}} > \frac{2}{3}.$$

So, as before, $G_n$ is convergent, since it is bounded below and monotonically decreasing.

I suspect this argument also adapts easily to the more general case $\sum_{k=1}^{n}\sqrt[r]{n},$ for $r \in \mathbb{N},$ where I'm guessing, we'll find $$1 + \sqrt[r]{2} + \dots + \sqrt[r]{n} \sim \frac{r}{r+1}n^{(r+1)/r} + \frac{\sqrt[r]{n}}{2} + C,$$ where $C = \zeta(-1/r).$ However, I confess to not having checked the details of this further generalisation.

Answer 3

The "sophisticated" way to do this is using the Euler-Maclaurin formula - look under the heading "Asymptotic expansion of sums". You'll want to start your sum at 1, not at 0, to avoid dividing by zero.

Answer 4

The standard approach should be along the lines of $\sum_{i\le n}\sqrt i=\sqrt n\sum_{i\le n}\sqrt{\frac{i}{n}}$, so $\frac1{n\sqrt n}\sum_{i\le n}\sqrt i=\sum_{i\le n}\sqrt{\frac{i}{n}}\frac1n\to\int_0^1\sqrt x{} dx=\frac23$, or $\sum_{i\le n}\sqrt i\sim\frac23 n\sqrt n$. What techniques do you know to estimate the error between integrals and their Riemann sums?

Answer 5

By the Euler-Maclaurin summation formula, we have

\begin{align}\sum_{k=1}^n\sqrt k&=\frac23n^{3/2}+\frac12n^{1/2}+\zeta(-1/2)+\sum_{k=1}^\infty\frac{B_{2k}\Gamma(\frac32)}{(2k)!\Gamma(\frac52-2k)}n^{\frac32-2k}\\&=\frac23n^{3/2}+\frac12n^{1/2}+\zeta(-1/2)+\frac1{24}n^{-1/2}+\frac1{1920}n^{-3/2}+\mathcal O(n^{-7/2})\end{align}

Seeing as the remainder term in the expansion goes to zero for $n\ge1$ and the collected constants add up to the zeta function.

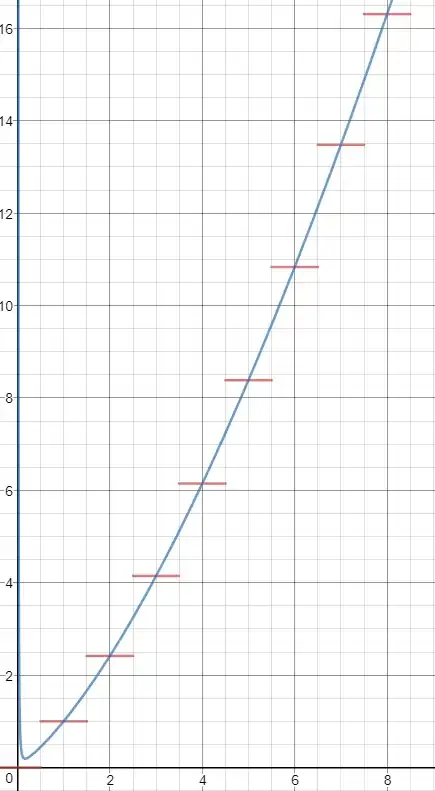
A graph of the terms as far as expanded is shown below:

More generally, we have, for $s\ne-1$ and large enough $n$,

$$\sum_{k=1}^nk^s=\zeta(-k)+\frac1{s+1}n^{s+1}+\frac12n^s+\sum_{k=1}^\infty\frac{B_{2k}\Gamma(s+1)}{(2k)!\Gamma(s+1-k)}n^{s-k}$$

As implimented in this graph.

Answer 6

Since square root is a monotonically increasing function, that summation will be between the integral of sqrt(i) from 0 to n and the integral of sqrt(i) from 1 to n-1.

Answer 7

You will find some really nice approximations at MathKB.

PS: You'll also find a couple of exact formulas there, though not written with elementary functions of course.