Taking Seats on a Plane

Question

This is a neat little problem that I was discussing today with my lab group out at lunch. Not particularly difficult but interesting implications nonetheless

Imagine there are a 100 people in line to board a plane that seats 100. The first person in line, Alice, realizes she lost her boarding pass, so when she boards she decides to take a random seat instead. Every person that boards the plane after her will either take their "proper" seat, or if that seat is taken, a random seat instead.

Question: What is the probability that the last person that boards will end up in their proper seat?

Moreover, and this is the part I'm still pondering about. Can you think of a physical system that would follow this combinatorial statistics? Maybe a spin wave function in a crystal etc...

Answer 1

Here is a rephrasing which simplifies the intuition of this nice puzzle.

Suppose whenever someone finds their seat taken, they politely evict the squatter and take their seat. In this case, the first passenger (Alice, who lost her boarding pass) keeps getting evicted (and choosing a new random seat) until, by the time everyone else has boarded, she has been forced by a process of elimination into her correct seat.

This process is the same as the original process except for the identities of the people in the seats, so the probability of the last boarder finding their seat occupied is the same.

When the last boarder boards, Alice is either in her own seat or in the last boarder's seat, which have both looked exactly the same (i.e. empty) to her up to now, so there is no way poor Alice could be more likely to choose one than the other.

Answer 2

This is a classic puzzle!

The answer is that the probability that the last person ends in up in their proper seat is exactly $\frac{1}{2}$.

The reasoning goes as follows:

First observe that the fate of the last person is determined the moment either the first or the last seat is selected! This is because the last person will either get the first seat or the last seat. Any other seat will necessarily be taken by the time the last person gets to 'choose'.

Since at each choice step, the first or last is equally probable to be taken, the last person will get either the first or last with equal probability: $\frac{1}{2}$.

Sorry, no clue about a physical system.

Answer 3

Let's find the chance that any customer ends up in the wrong seat.

For $2\leq k\leq n$, customer $k$ will get bumped when he finds his seat occupied by someone with a smaller number, who was also bumped by someone with a smaller number, and so on back to customer $1$.

This process can be summarized by the diagram $$1\longrightarrow j_1\longrightarrow j_2\longrightarrow\cdots\longrightarrow j_m\longrightarrow k.$$
Here $j_1<j_2<\cdots <j_m$ is any (possibly empty) increasing sequence of integers strictly between $1$ and $k$. The probability of this sequence of events is $${1\over n}\times{1\over(n+1)-j_1}\times {1\over(n+1)-j_2}\times\cdots\times{1\over(n+1)-j_m}.$$

Thus, the probability that customer $k$ gets bumped is $$p(k)={1\over n}\sum\prod_{\ell=1}^m {1\over(n+1)-j_\ell}$$ where the sum is over all sets of $j$ values $1<j_1<j_2<\cdots <j_m<k$. That is, \begin{eqnarray*} p(k)&=&{1\over n}\sum_{J\subseteq\{2,\dots,k-1\}}\ \, \prod_{j\in J}{1\over (n+1)-j}\cr &=&{1\over n}\ \,\prod_{j=2}^{k-1} \left(1+{1\over (n+1)-j}\right)\cr &=&{1\over n}\ \,\prod_{j=2}^{k-1} {(n+2)-j\over (n+1)-j}\cr &=&{1\over n+2-k}. \end{eqnarray*}

In the case $k=n$, we get $p(n)=1/2$ as in the other solutions. Maybe there is an intuitive explanation of the general formula; I couldn't think of one.

---

Added reference: Finding your seat versus tossing a coin by Yared Nigussie, American Mathematical Monthly 121, June-July 2014, 545-546.

Answer 4

This analysis is correct, but not complete enough to convince me. For example, why is the fate of the last person settled as soon as the first person's seat chosen? Why will any other seat but the first person's or the last person's be taken by the time the last person boards?

I had to fill in the holes for myself this way...

The last person's fate is decided as soon as anybody chooses the first person's seat (nobody is now in a wrong seat, so everybody else gets their assigned seat, including the last person) or the last person's seat (the last person now won't get their correct seat). Any other choice at any stage doesn't change the probabilities at all.

Rephrasing... at each stage, either the matter gets settled and there is a 50/50 chance it gets settled each way for the last person's seat, or the agony is just postponed. The matter can thus be settled at any stage, and the probabilities at that stage are the only ones that matter -- and they are 50/50 no matter what stage. Thus, the overall probability is 50/50.

Answer 5

Let $P(n)$ denote the probability of the last passenger getting his seat if we begin with $n$ passengers.

Consider the simple case for just $2$ seats:

$P(2) = \frac12$ (first boarder picks his own seat with 1/2 probability)

For $n$ seats: (i) With $\frac1n$ probability, the passenger picks the seat of the first passenger, the n'th seat from the end (in which case the last passenger would definitely get his seat). (ii) With 1/n probability, the current passenger picks the seat of the last passenger, first seat from the end (and now, the last passenger can definitely not get his own seat). (iii) Otherwise, the passenger picks some other seat (say #i from the end) among the n-2 remaining seats (with probability 1/n), continuing the dilemma. The problem now reduces to the initial problem with i seats.

Therefore, $$ P(n) = \frac1n \times 1 + \frac1n \times 0 + \frac1n\sum_{i=2}^{n-1} P(i) $$ or $$ nP(n) = 1 + \sum_{i=2}^{n-1} P(i).$$ So $$nP(n)-(n-1)P(n-1)=P(n-1)\Longleftrightarrow P(n)=P(n-1),$$ and $P(n)=P(2) = \frac12, \,\forall n \ge 2$.

Answer 6

I tried to synthesize the proof for myself from stuff I've read to get rid of all calculations (somehow I found the argument that "each person's choice is 50-50 between good and bad once we throw away the irrelevant stuff" convincing but hard to formalize).

Claim 1: when the last passenger boards, the remaining empty seat will either be his own or the first passenger's.

Proof: If the remaining empty seat belongs to passenger $n \neq 1, 100$, then passenger $n$ should have sat there.

Claim 2: if at any time a passenger other than the final passenger finds her seat occupied, then both the seat assigned to the first and to the final passenger will be free.

Proof: If not, then there is a nonzero probability that after this passenger makes a decision, both the first and last seats will be occupied. This contradicts Claim 1.

Claim 3: There is a bijection between the set of admissible seatings in which the final passenger gets his seat and the set where he doesn't.

Proof: Suppose for an admissible seating $S$ that passenger $n$ is the first to choose one of {first passenger's seat, last passenger's seat}. By claim $2$, there is a unique admissible seating $T$ which agrees with $S$ except that passenger $n$ and the final passenger make the opposite decision ($T$ matches $S$ until passenger $n$ sits, then by Claim 2, $T$ must continue to match $S$ until the final passenger).

Answer 7

I don't really have the intuition for this, but I know the formal proof. This is equivalent to showing that the probability that in a permutation of $[n]$ chosen uniformly at random, two elements chosen uniformly at random are in the same cycle is $1/2$. By symmetry, it's enough to show that the probability that $1$ and $2$ are in the same cycle is $1/2$.

There are many ways to show this fact. For example: the probability that $1$ is in a cycle of length $k$ is $1/n$, for $1 \le k \le n$. This is true because the number of possible $k$-cycles containing $1$ is ${n-1 \choose k-1} (k-1)! = (n-1)!/(n-k)!$, and the number of ways to complete a permutation once a $k$-cycle is chosen is $(n-k)!$. So there are $(n-1)!$ permutations of $[n]$ in which $1$ is in a $k$-cycle. Now the probability that $2$ is in the same cycle as $1$, given that $1$ is in a $k$-cycle, is $(k-1)/(n-1)$. So the probability that $2$ is in the same cycle as $1$ is $$ \sum_{k=1}^n {k-1 \over n-1} {1 \over n} = {1 \over n(n-1)} \sum_{k=1}^n (k-1) = {1 \over n(n-1)} {n(n-1)\over 2} = 1/2. $$

Alternatively, the Chinese restaurant process with $\alpha = 0, \theta = 1$ generates a uniform random permutation of $[n]$ at the $n$th step; $2$ is paired with $1$ at the second step with probability $1/2$. This is a bit more elegant but requires some understanding of the CRP.

Answer 8

There are many ways to come up with this answer, but here’s one that makes sense to me. For ease of explanation we’ll say that I’m the first person to sit down and you’re the last. Also if you sit in your own seat then you “win”, otherwise you “lose”.

Let’s say that there are only two seats, yours and mine. If I sit in my own seat, you win. If I sit in your seat, you lose. So you have a $50\%$ chance of winning.

Now let’s go back to $100$ seats. The previous paragraph still holds true: you have a $50\%$ chance of winning if we only consider your seat and mine. Now if I sit anywhere else, I’m just postponing the decision. Let’s say I sit in the seat of the person who’s 13th in line. Persons $2$ through $12$ will sit in their own seats, then when person $13$ comes in he can either sit in my original seat (and you win) or yours (and you lose). Or of course he could sit anywhere else and postpone the decision again.

If this keeps going, then eventually there are only two seats left and person $99$ is forced to choose either your seat or mine, again with 50% chance. There are only two seats that matter throughout the game: yours and mine. Any sitting in other seats is just postponing the decision of which of the two interesting seats gets sat in first. Note also that you’ll only ever end up in your seat or mine, no one else’s.

It’s a bit like flipping a coin, except that you can postpone flipping, but not indefinitely. What’s the chance of coming out heads? Well $50\%$, the postponement doesn’t change that.

Here’s a mathematical way to see it. Define $f(n)$ to be the chance that the last person in an airplane of n seats will get his own seat. It can be defined recursively like this: $$f(n)=\frac1n\cdot1+\frac{n−2}n\cdot f(n−1) + \frac1n\cdot 0$$

The first term is the chance that the first person will sit in his own seat $\frac1n$ multiplied by the chance, then, that the last person will sit in his own $1$. The last term is the chance that the first person will sit in the last person’s seat $\frac1n$ multiplied by the chance, then, that the last person will get his own seat $0$. The middle term counts every other seat. There are $n−2$ other seats, and there’s a $\frac1n$ chance of each, and they all simplify to the $f(n−1)$ case. Also $f(2)=0.5$.

If you plug in $0.5$ for the $f(n−1)$ term, you find that $f(n)=0.5$, so it’s true for any $n>1$.

Answer 9

This problem appears in Blitzstein's Introduction to Probability (2019 2 ed) Ch 1, Exercise 61, p 42. Here's the answer from p 10 of the Selected Solutions PDF.

Solution: The seat for the last passenger is either seat 1 or seat 100; for example, seat 42 can’t be available to the last passenger since the 42nd passenger in line would have sat there if possible. Seat 1 and seat 100 are equally likely to be available to the last passenger, since the previous 99 passengers view these two seats symmetrically. So the probability that the last passenger gets seat 100 is 1/2.

This solution doesn't satisfy me, because I couldn't get the symmetry argument and I didn't understand why "seat 42 can't be available". Here's how I convinced myself.

---

Let's call the first passenger $P_1$. There are 100 possible seats $S_i\:(i=1,2...100)$ she can randomly select. First let's cover the two "edge" cases, seat 1 and seat 100. Suppose she selects $S_1$ by chance. For notation purposes we'll say $S_1=P_1$ using equality operator as seat selection. If this happens there is no change in seating order, $P_2=S_2$, $P_3=S_3$, and eventually $P_{100}=S_{100}$. In the other "edge" case, $P_1=S_{100}$. In this case it should be clear that $P_2=S_2$, $P_3=S_3$, and so on. When $P_{100}$ gets on the plane she realizes that her seat is taken and the only available option is $S_1$ so $P_1=S_1$. Notice that the probability of $P_{100}=S_1$ and $P_{100}=S_{100}$ are the same for these two cases. Further notice I am not saying the probability of each occurence is 1/2. Clearly the probability of each of these events is 1/100 or 1/n, where n is in general the number of seats. It will turn out that n does not matter due to symmetry, which will be the fundamental insight into this problem. For now let's continue with more concrete cases...

Let's assume that $P_1=S_{99}$. Again, note that there is a 1/n chance of this seat selection, same as all the other seats. When $P_2$ boards the plane, she is able to take her seat $P_2=S_2$. Similarly, $P_3=S_3$ and so on until $P_{98}=S_{98}$. Ok, now $P_{99}$ boards the plane and sees $S_1$ and $S_{100}$ are the only two available seats. Her own seat was taken by $P_1$. She now must randomly choose. Clearly, given the previous seating order there is now a 50/50 chance that either $P_{99}=S_{1}$ or $P_{99}=S_{100}$. If $P_{99}=S_{1}$ then $P_{100}$ gets to sit in her assigned seat ($P_{100}=S_{100}$), otherwise she must sit in seat 1, so $P_{100}=S_{1}$. Note that the final 50/50 choice between $S_1$ and $S_{100}$ is the "game" that other answers have referred to here. It also provides the recursive base case that many answers here discuss. To see this, let's play another "game" and see what happens.

Let's now assume that $P_1=S_{98}$. Similar to above, $S_1$ is left open, $P_2=S_2$, $P_3=S_3$ and so on until $P_{97}=S_{97}$. Now, $P_{98}$ boards the plane and see that $S_1$, $S_{99}$, and $S_{100}$ are available. Well, let's go through these 3 possible choices. Assume $P_{98}=S_1$. Now, $P_{99}=S_{99}$ and $P_{100}=S_{100}$. The "game" ends with Passenger 100 getting their assigned seat. Continuing, imagine $P_{98}=S_{100}$. In that scenario, $P_{99}=S_{99}$ and $P_{100}=S_1$. In this case the game ended with Passenger 100 sitting in Seat 1. Notice that the probability of each outcome was exactly the same. Ok, one last possibility. Let's imagine that $P_{98}=S_{99}$. Ahhhh, now we've "kicked" $P_{99}$ out of her seat, and when she boards the plane she must choose between $S_1$ and $S_{100}$. Hey wait a minute. Didn't we already cover that case? Yes! And so here we are. Hopefully, by now you can recognize the recursion in this problem, the base case, the symmetry, and the "game" that every single simulation will play out the same way with Passenger 100 having equal probability of sitting in Seat 1 or Seat 100, with absolutely zero probability of sitting anywhere else. Therefore P=1/2!

Tada!

Answer 10

It is possible to count the different configurations of interest to calculate the probability directly, by formalizing some of the ideas already presented.

In an allowed configuration, denote a displacement of one or more passengers with the diagram $i\rightarrow j$ whenever passenger $i$ displaces passenger $j$ from their assigned seat ($i < j$).

Suppose C is an allowed configuration with a displacement D of passengers, say, $...i\rightarrow j...$ Clearly i has a predecessor (which can be added to the diagram) or i is passenger 1, since the problem states that only passenger 1 is free to displace passengers without being displaced themselves. Since each predecessor must represent a passenger who boarded earlier, of which there are a finite number, using this argument at most i times, shows that D must begin with passenger 1. By a similar argument, D must have a last passenger which chooses passenger 1’s seat to end the displacement.

If E is a displacement in C, by the same argument it must start with passenger 1, followed by the choices already indicated in D, so that E is the same as D. Clearly, two allowed configurations are the same if and only if their displacements are the same. Additionally, note that a displacement of the form, $\textstyle\ 1\rightarrow i \rightarrow … \rightarrow j$ where {i,…,j} is a subset of {2,…,100} in increasing order, always specifies a valid configuration. Hence,

There is a bijection between the set of allowable configurations and diagrams of the form $1\rightarrow i \rightarrow … \rightarrow j$ where {i,…,j} is a subset of {2,…,100} in increasing order.

Now count configurations by counting the diagrams. Write 1 as the diagram for the null displacement in the configuration where all passengers sit in their assigned seats. Note that this is same as counting all subsets of a two particular sets, so the probability that the final passenger is sitting in their assigned seat is:

$\textstyle \frac{\textrm{Number of all diagrams of the form } 1\rightarrow i \rightarrow … \rightarrow j\textrm{ where {i,…,j} is a subset of {2,…,99} in increasing order}}{\textrm{Number of all diagrams of the form } 1\rightarrow k \rightarrow … \rightarrow l\textrm{ where {k,…,l} is a subset of {2,…,100} in increasing order}} = \frac{2^{98}}{2^{99}} = \frac{1}{2}\\$

EDIT: This is not new, but for completeness sake ... After the 4th paragraph second sentence, it's clear that each allowable configuration can be identified by its unique displacement (chain). (Take the allowable configuration--seating chart--that has each passenger in their own seat to be the null displacement, so that every allowable configuration has exactly one displacement).

Then, for each displacement that ends in 100, 100 sits in seat 1 (end of induction/paragraph 3). For each displacement not ending in 100, passenger 100 sits in their own seat. Since every allowable configuration contains one displacement, then passenger must sit in seat 1 or 100.

As other's have noted (e.g. Will, Hunter), we can pair up each displacement $D$ with another equally likely: $\textstyle\ 1\rightarrow i \rightarrow … \rightarrow j$ pairs up with $\textstyle\ 1\rightarrow i \rightarrow … \rightarrow j \rightarrow 100$ since at the point j chooses seat 1, they could have chosen seat 100 with equal probability. The result immediately follows then since in any allowable configuration it's equally likely that passenger 100 is in their own seat or seat 1.

But to be pedantic, $$ \Pr(\text{$100$ gets their assigned seat}) $$ $$ =\sum_{\textrm{D does not end in 100}}^{}\Pr(\text{$D$}) $$ $$ =\textstyle \frac{\sum_{\textrm{D does not end in 100}}^{}\Pr(\text{$D$})}{\sum_{\textrm{D does not end in 100}}^{}\Pr(\text{$D$}) + \sum_{\textrm{D ends in 100}}^{}\Pr(\text{$D$})} $$ by pairing $$ =\textstyle \frac{\sum_{\textrm{D does not end in 100}}^{}\Pr(\text{$D$})}{\sum_{\textrm{D does not end in 100}}^{}\Pr(\text{$D$}) + \sum_{\textrm{D does not end in 100}}^{}\Pr(\text{$D$})} $$ $$ =\textstyle \frac{1}{2} $$

Answer 11

I thought I'd add another solution that uses recursion. Let $p_n$ be the probability that the n-th person gets the n-th seat (his own seat) and $q_n=1-p_n$ the probability that he does not. Then,

$$ p_n=\underbrace{1/n}_{\text{1-st person sits in 1-st seat}}+\underbrace{(n-2)/n}_{\text{1-st person does not sit in the 1-st or n-th seat}} \times p_{n-1} $$ $$ q_n=\underbrace{1/n}_{\text{1-st person sits in n-th seat}}+\underbrace{(n-2)/n}_{\text{1-st person does not sit in the 1-st or n-th seat}} \times q_{n-1} $$ Now substitute in $q_n=1-p_n$ to get $p_n=q_n=1/2$.

Edit: I should add that initially I just thought it was as simple as plugging one equation into the other but indeed an inductive argument is needed like @ely's answer.

Edit: my answer assumes that $p_i=p_j$ - basically I haven't taken into account that probabilities might be different depending on which seat the 1-st person sits in (as stated by @hans)... The answer might be salvageable if one instead defines $p_n$ as the probability that everyone on a plane with $n$-seats all sit in their own seat but not sure as this might make some other implicit assumption.

Answer 12

I know I am late to this question but I came here as a result of a link from this closed question: 100 seats Quant problem

I believe this is simpler than the solutions I see. Imagine that we simulate a coin toss with a wheel with three outcomes: red, white and blue.

We let red be heads and white be tails. If we get a blue, we spin again. That's exactly what is happening in this problem.

If the first person, chooses his own seat then everyone else, including the last person, will get his own seat. If the first person chooses the last seat then the last person doesn't get his seat. Otherwise, the first person chooses another seat and the game continues.

Everyone gets their own seat up to the person that was chosen in the first round. Let's say the first person chose $47$, for example, Then seats $2$ through $46$ will have their rightful owners and person $47$ will have to choose. His choices are $1$, $100$ or something else. In each case, if $1$ is chosen then the last person gets his seat, if $100$ is chosen, he doesn't get his seat and if something else is chosen then the game continues.

In this sense, we are essentially spinning the wheel until we get either a $1$ or $100$ so the probability that the last person gets his seat is $\frac{1}{2}$.

Answer 13

The other answer that uses recursion to define $p_{n}$ and $q_{n}$ is very light on details and makes it sound as if you can directly solve of $p_{n} = q_{n}$ from the two equations.

Note that the two equations

$$p_{n} = \frac{1}{n} + \frac{n - 2}{n}p_{n-1}$$ $$q_{n} = \frac{1}{n} + \frac{n - 2}{n}q_{n-1}$$

don't offer independent constraints on the variables since $p_{n} = 1 - q_{n}$. So subtract the equations $p_{n} - q_{n}$:

$$p_{n} - q_{n} = \frac{1}{n} + \frac{n - 2}{n}p_{n-1} - \frac{1}{n} - \frac{n - 2}{n}q_{n-1}$$ $$p_{n} - q_{n} = \frac{n - 2}{n}(p_{n-1} - q_{n-1})$$

At this point we can state for the base case, $n=2$, we know $p_{2} = q_{2} = \frac{1}{2}$. Now if we assume $q_{n-1} = p_{n-1}$, clearly the right-hand side of our last equation becomes zero, and $q_{n} = p_{n}$.

Since $q_{n} + p_{n} = 1$, then $\boxed{p_{n} = q_{n} = \frac{1}{2}}$.

It's just important to note that after setting up the problem recursively, you still need to appeal to induction to derive the solution. It's not as simple as algebraic manipulation of the definition of $p_{n}$ or $q_{n}$ even though this is how the other solution makes it sound.

Answer 14

Call the passengers $P_1,\dots,P_n$ in the order in which they board, and let $S_i$ be the seat assigned to $P_i$.

Consider the first moment at which a passenger $P_i$ sits in either $S_1$ or $S_n$. The other one of those seats is empty, so the passengers haven't all boarded yet, so $i\ne n$.

If $i=1$, $P_i$ takes a random seat as per the OP.

Otherwise, $i\ne 1$ and $i\ne n$, so the reason why $P_i$ picked $S_1$ or $S_n$ is that $S_i$ was already occupied. So in this case, $P_i$ takes a random seat as per the OP.

Thus in both the above cases, this moment is when a passenger takes a random seat. They are equally likely to pick $S_1$ as $S_n$. Thus each of the two cases below occurs with probability $1/2$.

If $P_i$ picked $S_n$, then $P_n$ will not get their assigned seat $S_n$.

If $P_i$ picked $S_1$, then the cycle of displacement of Bruce's proof ends, and everyone who has not yet boarded gets their assigned seat, including $P_n$.

Thus the answer is $1/2$.

Answer 15

Here is a simple proof. For $k\ge 2$, let $p_k$ be the probability that the $k$-th person's seat is taken when he/she tries to sit.

We consider the disjoint events that person $j$ takes up this particular seat, for $1\le j \le n$. In order for that to happen, $j$'s seat has to be taken, and then $j$ is left with $n-j+1$ random choices of which $j$ must take $k$'s seat. We can write: $$p_{k}={1\over n}+p_2{1\over n-1}+p_3{1\over n-2}\dots+p_{k-1}{1\over n-k}.$$

Thus, $p_2={1\over n}$, $p_3={1\over n}+{1\over n(n-1)}={1\over n-1}$. In general, $p_k={1\over (n-k+2)}$.

Answer 16

A recursive solution: Once a passenger who has been displaced from their assigned seat sits in the seat assigned to passenger $1$, no more passengers will be displaced. But if the displaced passenger takes some other seat, a passenger still standing in line will become displaced

Let the plane have $N$ seats and let $r_n$, $1\le n\le N-1$, be the probability that with $n$ passengers standing in line none of the standing passengers is displaced from their assigned seat. We have $r_{N-1}=\frac{1}{N}$ because that is the probability the first passenger happens to choose their own seat. If $n$ passengers are standing in line and somebody in line is displaced—it will always be exactly one passenger—the probability that the displaced passenger is at the head of the line is, by symmetry among the standing passengers, $\frac{1}{n}$. And if the displaced passenger is at the head of the line, the probability that they take the seat assigned to passenger $1$ is also $\frac{1}{n}$. It follows that $$ r_{n-1}=r_n+\frac{1-r_n}{n^2}. $$ By induction, we find that $r_n=\frac{1}{n+1}$ and hence $r_1=\frac{1}{2}$.

Another recursive solution: This expands on Shashank's answer, emphasizing a key point that caused me some confusion at first.

When a non-displaced passenger gets to the head of the line, they simply take their assigned seat, but when a displaced passenger gets to the head of the line, they choose uniformly at random from the set $$ \{\text{passenger 1's seat}\}\cup\{\text{seats assigned to passengers standing behind them in line}\}. $$ Although technically passenger $1$ is not displaced, they follow the same procedure as the displaced passengers do, so we lump them in with that group. As a consequence, if passenger $k$ is displaced, then when that passenger gets to the head of the line, the situation is just like the original problem, but for a plane of $N-k+1$ passengers.

Define $p_n$ to be the probability that, in the setup described, the last passenger to board an $n$-seat airplane gets their assigned seat. Then for $n\ge2$, $$ p_n=\frac{1}{n}\cdot1+\left[\frac{1}{n}\sum_{k=2}^{n-1}p_{n-k+1}\right]+\frac{1}{n}\cdot 0. $$ Each term in this expression corresponds to a seat choice of passenger $1$: if the choice is seat $1$, passenger $n$ gets their assigned seat with probability $1$; if it's seat $k$, for $2\le k\le n-1$, then passengers $2$ through $k-1$ take their assigned seats and, when passenger $k$ comes to choose a seat, it is like the original problem but with $n-k+1$ seats; if the choice is seat $n$, then passenger $n$ gets their assigned seat with probability $0$.

Multiplying by $n$ and reversing the order of summation gives $$ np_n=1+\sum_{k=2}^{n-1}p_k. $$ Subtracting this from the same recurrence with $n$ replaced by $n+1$ gives $$ (n+1)p_{n+1}-np_n=p_n, $$ for $n\ge2$. Hence $p_2=p_3=p_4=\ldots$. One easily sees $p_2=\frac{1}{2}$.

The stumbling block for me was in seeing the similarity between passenger $1$ and the displaced passengers. Passenger $1$ chooses randomly among the available seats, which include their assigned seat, and I got hung up on the possibility that passenger $1$ might get their own seat, which can't happen for other displaced passengers. That, however, is not the correct parallel to draw. The right parallel is that both passenger $1$ and the displaced passengers can get passenger $1$'s seat, which ends the cycle of displacement.

Several other answers on this page, like (this, this, and this) —jump straight to an even simpler recurrence. The recurrence does hold and can be derived from this one, but haven't been able to understand how to get that recurrence directly. This issue was raised by Hans on this page in a number of his comments. If I stumble upon any insight that might help other readers with this point, I will add it here.

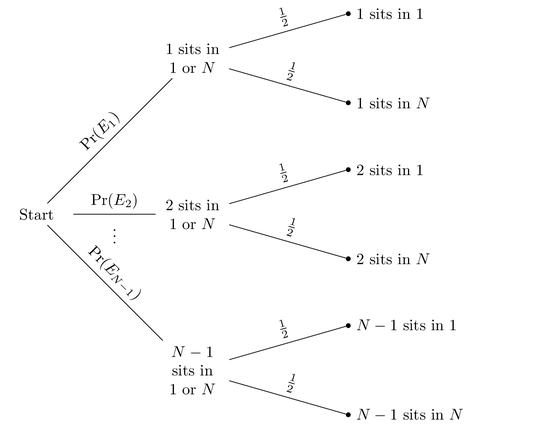
Solution using conditional probability: we have seen that if seat $1$ is chosen before the last passenger is seated, then that passenger sits in their assigned seat; if seat $N$ is chosen before the last passenger is seated, then the last passenger is displaced and must take seat $1$. Let $E_k$ be the event that the $k$th passenger to be seated is the first to take one of seats $1$ and $N$. Then $$ \Pr(\text{$N$ gets their assigned seat})=\sum_{k=1}^{N-1}\Pr(\text{$k$ sits in $1$}\mid E_k)\Pr(E_k)=\frac{1}{2}\sum_{k=1}^{N-1}\Pr(E_k)=\frac{1}{2}. $$ Diagrammatically, this calculation is shown below. The probability that $N$ gets their assigned seat is the sum of the probabilities that each of passengers $1$ through $N-1$ takes seat $1$.

Solution using a bijection between cycles: (This completes a final, needed step in hunter's answer.) The seating process results in a permutation of the passengers, and this permutation always consists of a single cycle containing passenger $1$ followed by displaced passengers, an ascending order. So for $N=100$ the cycle $(1,46,53,75,88)$ represents the situation where passenger $1$ displaces passenger $46$, $46$ displaces $53$, $53$ displaces $75$, $75$ displaces $88$, and $88$ sits in passenger $1$'s seat. Passengers $89$ and up, and passenger $100$ in particular, will sit in their assigned seats. The cycle $(1,46,53,75,88,100)$ represents a similar situation, except that passenger $88$ displaces passenger $100$. Passengers $89$ through $99$ will sit in their assigned seats, and passenger $100$ will have only one choice of seat: passenger $1$'s seat.

The probability of occurrence of these two cycles is the same: $$ \frac{1}{100}\frac{1}{55}\frac{1}{48}\frac{1}{26}\frac{1}{13}. $$ In general, when displaced passenger $k$ chooses a seat, they choose uniformly at random from $101-k$ possible seats. Once passenger $88$ has chosen either seat $1$ or seat $100$ (each of which happens with probability $\frac{1}{13}$), the seating of the remaining passengers standing in line is determined. Now every cycle that does not contain $100$ is paired in this way with an equally probable cycle that does contain $100$. Hence passenger $100$ sits in their assigned seat with probability $\frac{1}{2}$.

Answer 17

As is sometimes the case it is easier to think about the inverse probability -- that you will not get your seat.

As time passes on more and more passengers fill the plane and so the probability of someone taking your seat increases. Probability is a function of time -- so this is a stochastic process.

At t=1: $$p(1)=\frac{1}{100}$$

At t=2: $$p(2)=p(1) + p(1) \frac{1}{99}$$ $$...$$ $$p(t)=p(t-1) \Big(1 + \frac{1}{101-t}\Big)$$ If we apply a brute force recursive technique $$p(1)=\frac{1}{100}$$ $$p(2)=\frac{1}{99}$$ $$p(3)=\frac{1}{98}$$ we can guess that the random process is: $$p(t)=\frac{1}{101-t}$$

Would love someone on here to provide a more rigorous, yet simple inductive solution, maybe using telescoping, as summation of left hand side differences collapses.

So all the guys who have boarded before me will create a situation for me where $$p(99)=\frac{1}{101-99}=\frac{1}{2}$$ And since I was originally asked the inverse probability: $$\bar{p} = 1 - p = 1 - \frac{1}{2}=\frac{1}{2}$$

Answer 18

My answer owes much to what went before , but it works for me. The first person in the queue ( assume he does not sit in his own seat by random chance) displaces one person still in the queue by sitting in their seat . Passengers continue to board in their own seats until the displaced person comes to sit down. His own seat is taken so he in turn displaces someone else who is in the queue. There is always one displaced person in the queue as this cycle continues From here there are only 2 possible outcomes, a) a displaced person randomly choses the first mans seat at which point the cycle of displacement ends and the boarding can then continue to the end person with everyone else including the last man getting their own seat or b) The last mans seat is selected by a displaced person then there is no more displacement until the last man tries to sit down and will find his seat full

Whichever of a ) or b ) happens first will determine whether the last mans seat is available when he comes to board. a) or b) are 2 events determined by random chance therefore each has 50% chance of happening Hence answer = 1/2 or 50%

Answer 19

I have come up with my own solution using a revolutionary war analogy, which is quite fun and intuitive I think.

We classify passengers as two groups: (i) "rebels": the first man and those who do not end up sitting at their own seats; (ii) "rulies": those who end up sitting at their own seat. We will refer to the First Man's seat as "the throne" due to its significance. We will refer to each passenger as "the n-th man" by their order of entrance. We will refer to appointment of the 100-th man (the one true saviour) as a rebel as ultimate victory of the rebellion. Anyone other than the saviour seating on the throne will doom the revolution.

Each rebel (assuming he is the n-th man, including the first man) has 3 choices:

(i) Doom the rebellion: with probability $\frac{1}{101-n}$, sit at the throne and thus effectively ending the rebellion and ensure no more rebels thereafter; this fails the rebellion

(ii) Win the rebellion: with probability $\frac{1}{101-n}$ appoint the 100-th man, the saviour, as rebel by sitting at 100-th man's seat, thus winning the rebellion;

(iii) Leave it to future generations: with remaining probability, appoint a rebel other than the saviour and thus does not doom or win the rebellion on his watch.

We can see that we have equal chance to win the rebellion or lose it under each rebel's command. So the result is with probability $1/2$ we lose the rebellion, which is the event the last passenger sits at his own seat.

Answer 20

There are two sub problems. First to show that person $n$ has only two choices. Second to show that the probability is $\frac{1}{2}$. The first doesn't immediately imply the second.

sub-problem 1: When person $n$ boards, then he will not find seat $n-1$ empty. Why? If $n-1$ was empty when $n$ boards, it was also empty when $n-1$ boarded and he ($n-1$) would have taken seat $n-1$.

Similarly, when person $n$ boards, then he will not find seat $n-2$ empty. Why? If $n-2$ was empty when $n$ boards, it was also empty when $n-1$ and $n-2$ boarded and he ($n-2$) would have taken seat $n-2$.

Hence when person $n$ boards, the only seats that can possibly be available are either seat $1$ or seat $n$.

sub-problem 2: It is easier with example. The possible options for $n=4$ are:

1234

2134
3124
4123
4132

4213
3214

4231

Notice the location of person $1$.
seat $1$: $2^0$
seat $2$: $2^2$
seat $3$: $2^1$
seat $4$: $2^0$

So when person $1$ is seated fixed in seat $2$, the problem of distributing the remaining persons $2,3,4$ will be the same as the original problem but with $3$ people (convince yourself) with $4$ being last half the time. And if person $1$ is fixed in seat $3$ (implies that person $2$ is seat $2$) this reduces to a problem with $n=2$ with person $4$ being last half the time.

By induction, if we assume number of ways for $n$ is $2^{n-1}$.

For $n+1$ people, we get total number by looking at location of person $1$:
seat $1$: $2^0$
seat $2$: $2^{n-1}$
seat $3$: $2^{n-2}$
seat $n+1$: $2^0$

with total being $2^n -1 +1 = 2^n$ and half the time last person is in last location.

Interestingly, other than person $1$, each person is in their assigned seat half the time.

Answer 21

Here is my sloppy python code I made concerning this interesting problem:

import random
num_simulations = 100000
yes = 0
no = 0
airplane_passengers = list(range(100))
for _ in range(num_simulations):
    airplane_seats = list(range(1, 101))  # Reset seats for each simulation
    available_seats = airplane_seats.copy()
    available_seats.remove(random.choice(available_seats)) # First passenger forgets his boarding pass
    random.shuffle(airplane_passengers)  # Shuffle the passenger order
    for i in airplane_passengers:
        if airplane_passengers[i] in available_seats:
            available_seats.remove(airplane_passengers[i])
        elif airplane_passengers[i] != available_seats:
            if available_seats:  # Check if available_seats is not empty
                x = random.choice(available_seats)
                available_seats.remove(x)
    if airplane_passengers[i] == 99:  # 100th passenger
        if airplane_seats[i] == 100:
            yes += 1
        else:
            no += 1
print(f"The probability that the last person that boards will end up in their proper seat: {yes/(yes+no)}")