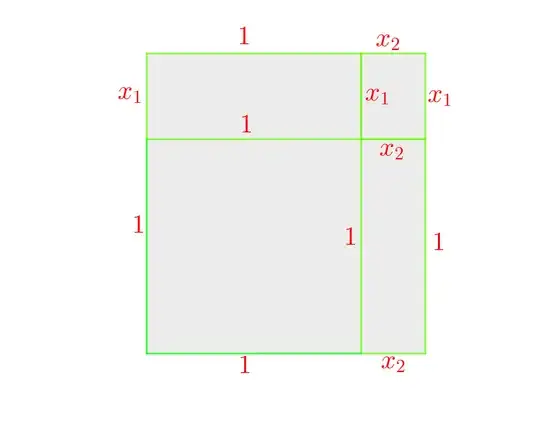
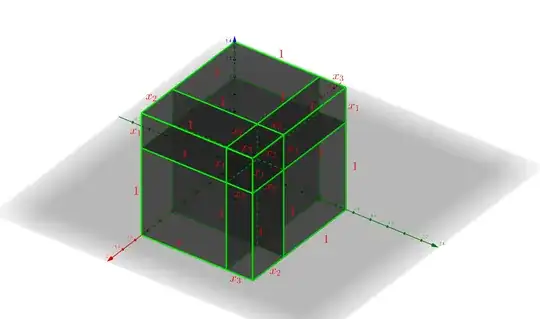
For an answer that a 16 year old may understand, you can consider this interpretation. Take a box with $n$ objects, and give the $i$th object the label $x_i$ (which you can think of as a letter).
Now consider picking (in no particular order) some elements in that box, and recording your choice. If you picked elements labeled $x_{i_1},\ldots,x_{i_k}$, then assign it the word $x_{i_1} \ldots x_{i_k}$ in the letters as above. This word corresponds to a set $J = \{i_1,\ldots, i_k\}$ with $k$ distinct elements contained in $\{1,\ldots,n\}$.
Takeaway 1. for each subset $J$ of the labels $\{1,\ldots,n\}$, we have created a word $x_J = x_{i_1},\ldots,x_{i_k} = \prod_{j\in J} x_j$, corresponding to a choice of objects in your box.
Now consider the expression $(1+x_1)\cdots (1+x_n)$, and what happens when you multiply it out. For each term $1+x_i$, you either have to choose to take $1$ or $x_i$. This choice corresponds to looking at the object $i$, and deciding if you are picking it from the box (take the term $x_i$) or not (take the term $1$).
Takeaway 2. Doing this in all possible ways ---that is, computing the product--- then effectively gives you the sum of all the words $x_J$ as $J$ runs through sets contained in $\{1,\ldots,n\}$.
It follows that $(1+x_1) \cdots (1+x_n) = \sum_{J\subseteq [n]} x_J$, like you wanted. You can also embellish this a bit:
$$(1+tx_1) \cdots (1+tx_n) = \sum_{J\subseteq [n]} x_J t^{|J|}$$
where now the $t$ variable keeps track of the number of times you did choose to pick an object of the box. In particular, the empty set $\varnothing$ corresponds to the term $1$, obtained by always picking $1$ in the left hand side. As an example, if you have three objects $x$, $y$ and $z$, you get
$$(1+tx)(1+ty)(1+tz) = 1 + (x+y+z)t +(xy+xz+yz) t^2+ xyzt^3.$$