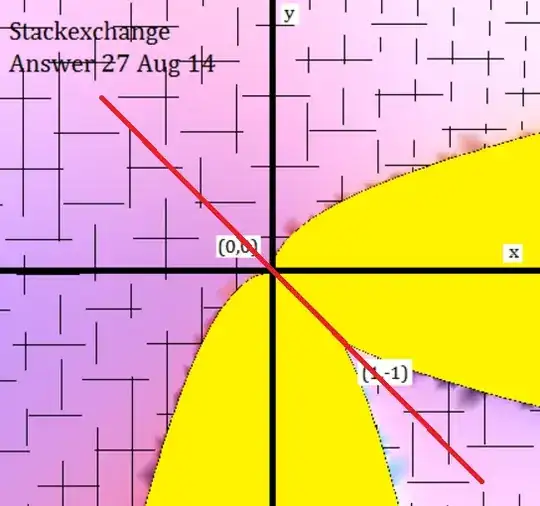
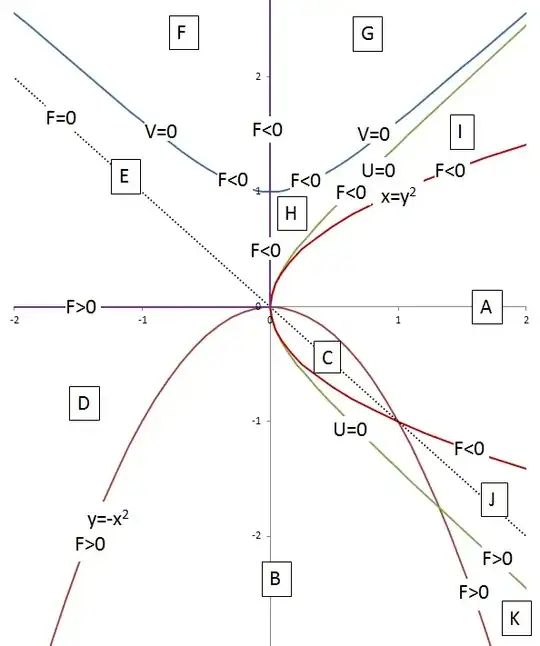
In the following proof we divide the $(x,y)$ plane into regions (see diagram) and show that each region can contain no solutions except on the line $x + y = 0$.
Let
$$
F(x,y) = U(x,y)V(x,y) – y
$$
where
$$
U(x,y) = \sqrt{y^2 – x} \,\, – x
\\V(x,y) = \sqrt{x^2 + y} \,\, – y
$$
Then solutions satisfy
$$
F(x,y) = 0
$$
Substituting $y=-x$ shows that $x+y=0$ is a solution for all x.
U is nonreal where $x>y^2$ (regions A and C in the diagram, bounded by red lines) and V is nonreal in the region $y<-x^2$ (regions B and C, also bounded by red lines). In these regions F is nonreal except possibly in region C, where U and V are both unreal. But there the condition for F to be real reduces to $x+y=0$, a subset of the known solution.
The following statements and deductions relate to the other regions of the $(x,y)$ plane, where $U$ and $V$ are real.
$U<0 \Leftrightarrow x>\tfrac{1}{2}(-1 + \sqrt{1 + 4y^2})$ (regions I, J).
$V<0 \Leftrightarrow y>\tfrac{1}{2}(1 + \sqrt{1 + 4x^2})$ (all regions except F, G).
$U_{x} < 0$ (regions D-K)
$V_{x} < 0 \Leftrightarrow x < 0$ (regions D, E, F)
$U_{xx} < 0$ (regions D-K)
$V_{xx} < 0 \Leftrightarrow y < 0$ (regions D, J, K)
where a subscript x denotes partial differentiation with respect to x.
On the diagram the lines on which $U=0$ and $V=0$ are coloured green and blue, respectively. It is easily shown that $F$ is nonzero on all the coloured lines (with sign as indicated) except at $(0,0)$ and $(1,-1)$. These lines delimit, but are excluded from, the regions A-K.
From the results above we can make the following deductions.
In region D:
$$
U>0, V>0, U_{x}<0, V_{x}<0
\\F_{x} = UV_{x} + VU_{x} < 0
$$
This region is bounded on the right by the line $y<-x^2$, on which $F>0$. So $F>0$ throughout region D and it can contain no solutions.
In region E:
$$
U>0, V>0, U_{x}<0, V_{x}<0
\\F_{x} < 0
$$
so here there can be no solutions other than those known to exist on the line $y=-x$.
In region F:
$$
U>0, V<0, U_{x}<0, V_{x}<0, U_{xx}<0, V_{xx}>0
\\F_{xx} = UV_{xx} + VU_{xx} + 2U_{x}V_{x} > 0
$$
This region is bounded on the left by the line $V=0$ and on the right by the line $x = 0$, and on both these lines $F<0$. So the positive second derivative $F_{xx}$ means there can be no solutions $F=0$ in this region.
In a similar way, solutions can be ruled out for the following regions:
In region G, bounded on right by the line $V=0$ on which $F<0$:
$$
U>0, V<0, U_{x}<0, V_{x}>0
\\F_{x}>0
$$
In region I, bounded on left by the line $U=0$ on which $F<0$:
$$
U<0, V>0, U_{x}<0, V_{x}>0
\\F_{x} < 0
$$
In region J, containing a segment of the known solution line $x+y=0$ on which $F=0$:
$$
U<0, V>0, U_{x}<0, V_{x}>0
\\F_{x} < 0
$$
In region K, bounded on the left and right by lines on which $F>0$:
$$
U>0, V>0, U_{x}<0, V_{x}>0, U_{xx}<0, V_{xx}<0
\\F_{xx} = UV_{xx} + VU_{xx} + 2U_{x}V_{x} < 0
$$
Finally, in region H:
$$
U>0, V>0, U_{x}<0, V_{x}>0
$$
and we note that $U_{x}<0$ in region G also, so for a given $y$,
$U<U_{max}$, where $U_{max} = U(0,y) = y$
For the same value of y, $V<V_{max}$, where $V_{max} = V(X,y)$, and X is the value of x on the right-hand boundary of the region. On this boundary, $y=\sqrt{X^2+X}$, so
$$
V_{max} = V(X,y) = \sqrt{X^2+y} \, – y
< \sqrt{X^2+X+y} \, - y = \sqrt{y^2 + y} \,\, – y < \tfrac{1}{2}.
$$
Therefore
$$
F = UV – y < U_{max} V_{max} – y < y \tfrac{1}{2} – y = \, –\tfrac{1}{2} y < 0
$$
which completes the proof that there are no solutions other than $x+y = 0$.