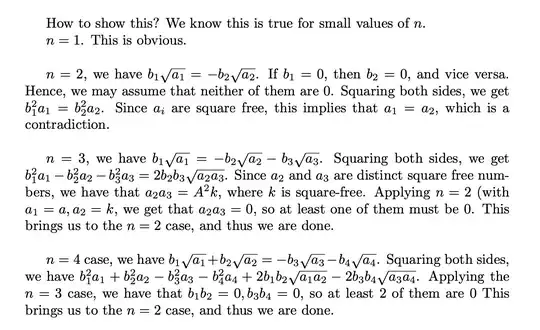The sum of the square roots of $n$ distinct squarefree integers is never an integer. Elementary proof

Question

I'm trying to prove that, if $k_1, \cdots k_n$ are distinct squarefree integers than $$ \sum_{i=1}^n \sqrt{k_i} \notin \mathbb{N} $$ without using the theory of algebraic extensions nor Galois theory. the usual proof is the following:

---

The theorem is true for $n=2$. Assume it is true for $n-1$ squarefree integers, than we have that $$ [ \mathbb{Q}(k_1, \cdots k_{n-1}) : \mathbb{Q} ]>1 $$ where $[K :L]$ is the degree of the field extension. Now assume $$ \sum_{i=1}^n \sqrt{k_i} \in \mathbb{N} $$ than $$ 1=[ \mathbb{Q}(k_1, \cdots ,k_{n-1},k_n) : \mathbb{Q} ]=[ \mathbb{Q}(k_1, \cdots ,k_{n-1},k_{n}) : \mathbb{Q}(k_1, \cdots ,k_{n-1} )] [ \mathbb{Q}(k_1, \cdots ,k_{n-1}) : \mathbb{Q} ] $$ where I have used the tower lemma. This is absurd and so the theorem is proved by induction (to be more precise this proves the theorem for any set of integers that are not perfect squares)

EDIT

I will give some intuition of the proof that $$\mathbb{Q}(\sqrt{k_1}, \sum_{i=2}^{n} \sqrt{k_i})=\mathbb{Q}(\sum_{i=1}^{n} \sqrt{k_i})$$

To do this i will use the following particular case of the primitive element theorem:

If $a,b$ are algebraic over a field of characteristic $0$ than $F(a,b)=F(c)$ for some $c \in F(a,b)$. Moreover if $f$ is the minimal polynmial of $a$ than $c=a+db$ where $d \in F$ is such that $a+db$ is not a root of $f$ in its splitting field

As the minimal polynomial of $\sqrt{k_1}$ is $x^2-k_1$ we see that, if $\sum_{i=2}^n \sqrt{k_i} \ne \pm 2\sqrt{k_1}$ we can choose $d=1$

I will not give the full proof of this, but the core is to show that, if we call $g$ the minimal polynomial of $b$ and $h(x):= f(a+d(b-x))$ we have $$ \gcd(g,h)=\gcd_{F(a+db)}(g,h)=x-b $$

that implies that $b \in F(a+db)$ and so $F(a,b) \subseteq F(a+db)$

---

here and here there are other proofs that still uses Galois theory of at least field extensions

Is there any elementary proof that can be understood by people without knowledge in abstract algebra ?

The case $n=2$ can be proven by squaring the sum, but already in the case $n=3$ I don't know how to prove it without using field extensions

Update

As said in the comments if the integers are pairwise coprime the case $n=3$ can be proved by using only elementary methods indeed by squaring both members of the equation $$ \sqrt{k_1}+\sqrt{k_2}=N-\sqrt{k_3} $$ and regrouping all the integer terms we have $$ 2\sqrt{k_1k_2} +2N \sqrt{k_3}=N_2 $$ squaring again both members we arrive to $8N \sqrt{k_1k_2k_3}=N_3$ that is never satisfied for pairwise coprime squarefree integers

Answer 1

Here are my notes from 10 years ago, which might have errors in them. I did not come up with this argument.
I know images aren't ideal, but I'm too lazy to type this up. Feel free to delete/edit/vote this solution as desired.

Note: Since 1 is (considered) a squarefree integer, OP's naive claim that $ \sqrt{ k_i } \not \in \mathbb{N}$ needs to be modified to remove $k_i = 1$.

(You can ignore the following note about how to use repeated squaring for $n \leq 4$. However, this doesn't extend to more variables.)

We're now ready to proof a slight variant of the theorem listed at the start, and is a slightly stronger statement than what OP asked for (as it allows for negative coefficients):

If $ \{ a_i \}$ are distinct numbers from the set $SF \backslash \{1 \}$, and $\{ b_i\}$ are any integers, then $ S = \sum b_i \sqrt{a_i } \in \mathbb{N}$ if and only if all $ b_i = 0 $ (and hence $ S = 0 $ ).

Motivation: The field theoretic idea here is that if $ S = \sum b_i \sqrt{a_i}$, then for any prime $ p \mid a_1$ replacing $\sqrt{p}$ with $ - \sqrt{p}$ throughout will still retain the validity of the expression. This implies that $ S = -b_1 \sqrt{a_i} + \sum \pm b_i \sqrt{ a_i } $ for a known set of $ \pm b_i$ where the signage depends only on whether $p \mid a_i $. Adding these two expressions, we get $ 2 S $ as the sum of fewer radical terms, so an induction approach could work.
We will merely show the weaker result that $ S = -b_1 \sqrt{a_1} + \sum_{i=2}^n \pm b_i\sqrt{a_i} $ for some suitable choice of signs, which is sufficient to add these expressions and reduce the number of terms.

The backwards part is obvious. We prove the forward part by induction.
Base case: If $ b_1 \sqrt{a_1} = S$ with $b_1 \neq 0$ then $b_1^2 a_1 = S^2$ and so $a_1 $ is a perfect square, which is not possible in $ SF \backslash \{ 1 \}$. Thus $b_1 = 0 $.

Induction step: Suppose it is true for $n-1$ summations.
Case 1: $ S = 0 $.
Multiply throughout by $\sqrt{a_i}$. Since $a_i \neq a_1$, so $ a_i a_1 = k_i^2 a_i'$ where $a_i' \in SF \backslash \{ 1 \}$.
Thus $\sum_{i=2}^n (b_i k_i) \sqrt{a_i'} = - b_1 a_1 \in \mathbb{N}$.
Applying the induction hypothesis, we get $ b_i' = 0 \Rightarrow b_i = 0 $ for $i = 2$ to $n$, and $ 0 = S = b_1 \sqrt{a_1} \Rightarrow b_1 = 0 $.

Case 2: $ S \neq 0 $.
Set up $F_{L(\sqrt{a_1}, \sqrt{a_2}, \ldots \sqrt{a_n} )} (T) $ from the previous discussion, so $F_{L(\sqrt{a_1}, \sqrt{a_2}, \ldots \sqrt{a_n} )} (S) = 0 $, and

$$ 0 = \sqrt{a_1} P(a_1, a_2, \ldots a_n, S) + Q(a_1, a_2, \ldots , a_n, S).$$

The polynomials $P$ and $Q$ have integer coefficients, so when evaluated at the integers will give us integer values, thus $ 0 = \sqrt{a_1} P^* + Q^*$ and hence these values are also 0. Thus, $ 0 = -\sqrt{a_1} P^* + S^*$.

Now, consider $$ \begin{array} { r l } G_L(T) & = \prod [ T + L'(x_1, x_2, \ldots, x_n) ] \\ & = \prod [ T - L'(-x_1, x_2, \ldots, x_n) ] \\ & = -x_1 P(x_1^2, x_2^2, \ldots , x_n^2, T) + Q(x_1^2, x_2^2, \ldots , x_n^2, T). \end{array} $$

Since $ 0 = - \sqrt{a_1} P^* + Q^* = \prod(S + L')$, so there exists some $S+L^* = 0$.
We have $S = -b_1 \sqrt{a_1} + \sum_{i=2}^{n} c_i \sqrt{a_i}$ where $ c_i \in \{ b_i, -b_i \}$.
Adding up the 2 expressions for $S$, we get that $2S = \sum_{i=2}^n (b_i + c_i) \sqrt{a_i}$ and hence by the induction hypothesis $2S = 0$.
This is a contradiction, so this case cannot occur.

---

Original version of the final part.

Answer 2

Distinct squarefree integers: $a_n$ with n=1..k, now first try:

$\sqrt{a_{1}}+\sqrt{a_{2}}=c$ with $c$ an integer at will.
$\sqrt{a_{2}}=-\sqrt{a_{1}}+c$ then square it:
$a_{2}=-2\sqrt{a_{1}}c+a_{1}+c^2$ -- since $a_1$ is a distinct squarefree integer this is not possible.

Again:
$\sqrt{a_{1}}+\sqrt{a_{2}}+\sqrt{a_{3}}=c$
$\sqrt{a_{2}}+\sqrt{a_{3}}=-\sqrt{a_{1}}+c$
$2\sqrt{a_{3}}\sqrt{a_{2}}+a_{2}+a_{3}=-2\sqrt{a_{1}}c+a_{1}+c^2$ and same on RHS as above -- not possible.

Continue ad libitum.