Given 5 points (every 5 points define a conic) find the foci of their conic using straightedge and compass construction.
I thought about this question a while ago and can't solve it. Hypothetically it's equivalent to finding roots of a quadratic, so it should be solvable but I'm not certain how. Algebraic approach seems like an awful thing to do here, so please don't unless certain there is no other way.
I'll show a possible (lengthy) solution below. I'm not going to prove all the constructions involved, but I can add some explanation on request.
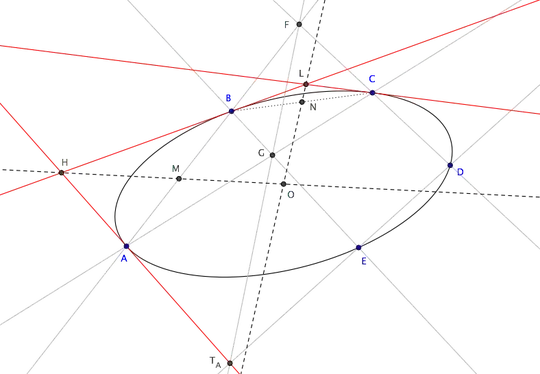
We start by finding the lines tangent to the conic at three points. Let $ABCDE$ be the five given points (see figure below). We can use Pascal's theorem to find the line tangent to the conic at $A$: if $F$ is the intersection of $AB$ with $CD$, and $G$ is the intersection of $AC$ with $BE$, then the intersection $T_A$ of $FG$ with $DE$ is a point on the tangent at $A$ to the conic $ABCDE$ (see here for a detailed proof). Repeat the same construction to find the lines tangent to the conic at $B$ and $C$ (red in the figure).
We can now find the center of the conic. Let $H$ be the intersection of the lines tangent at $A$ and $B$, and $L$ the intersection of the lines tangent at $B$ and $C$. If $M$ and $N$ are the midpoints of segments $AB$ and $BC$, then the center $O$ of the conic is the intersection of lines $HM$ and $LN$ (this is due to a another well-wknon theorem: center, midpoint of a chord and intersection of the tangents at the endpoints of the chord are collinear). If lines $HM$ and $LN$ are parallel then the conic is a parabola: in that case draw another tangent at $D$ and construct the focus as explained here.
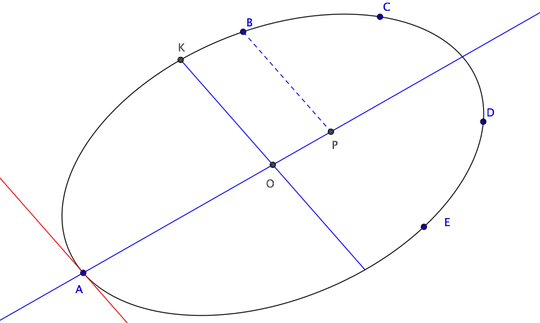
Let's now construct two semi-conjugate diameters of the conic. Having found the center $O$, draw through $B$ a line parallel to the tangent at $A$ (see figure below), intersecting line $OA$ at $P$. Draw then through $O$ a line parallel to the tangent at $A$ and a point $K$ on it such that
$$ OK={OA\cdot BP \over \sqrt{|OA^2-OP^2|} }. $$
Segments $OA$ and $OK$ form a couple of semi-conjugate diameters of the conic. The conic is an ellipse if $OA>OP$, while it is a hyperbola if $OA<OP$
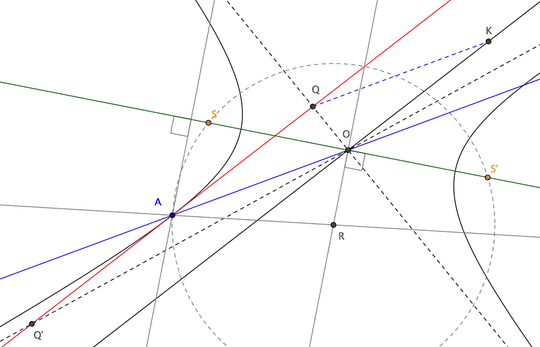
We can finally construct the foci of the conic. If the conic is an ellipse then you can find major and minor axes as explained here, and from them the foci.
If the conic is a hyperbola, then draw through $K$ the line parallel to $OA$ to meet at $Q$ the tangent through $A$, and reflect $Q$ about $A$ to $Q'$. Lines $OQ$, $OQ'$ are then the asymptotes of the hyperbola and its transverse axis is the bisector of $\angle QOQ'$ (green in figure below).
Foci $S$ and $S'$ are those points on the transverse axis lying at the same distance from $O$ and such that tangent $AQ$ is the bisector of $SAS'$. To construct them, draw from $A$ the line perpendicular to the transvere axis and reflect it about tangent $AQ$. Let then $R$ be the intersection of that reflected line with the perpendicular to the transverse axis from $O$. The circle through $A$ with center $R$ intersects then the transverse axis at $S$ and $S'$.
