Graphically locate the axes or foci of an ellipse from 5 arbitrary points on its perimeter.

Question

Five distinct non-collinear points are required to define an ellipse similar to the way that three non-collinear points define a circle and can be used to determine the center point of that circle. I have found many mechanical explanations showing how to draw an ellipse given the major axis, minor axis and/or foci as well as algebraic solutions for determining these key features given any 5 points on the ellipse. What I am trying to find is a geometric ruler and compass type method for locating the major and minor axes and foci of an ellipse when none of them are known, but given 5 points which are known to be on an arbitrarily positioned and oriented ellipse. Specifically, the ellipse's axes are not necessarily oriented in any particular relation to the X and Y coordinate axes. I am not looking for an algebraic solution to be plotted. I already have that capability. Rather, I am looking for a mechanical construction technique for locating the foci and/or the two axes from the 5 known points. Once I can locate the foci or axes of the ellipse, I can easily draw the remaining key points. Ruler and compass type construction is preferable, but pins-and-a-string or similar sort of solution would be a reasonable alternative. Can this be done? If not, can someone provide a proof that it is impossible? Thanks.

Answer 1

Introduction

In what follows, I make many statements without proof. Regard those as suggestions of exercises. I also neglect some exceptional cases, e.g. where the conic degenerates. Nevertheless, you are invited to think about what happens in such cases.

In contrast to classic treatises, the methods presented here are not optimized for expediency in drawing, but for recognization of a few essential principles. Unless noted otherwise, the methods work for ellipses as well as for hyperbolas. Applying the methods to parabolas results in a few particularities which are presented as well.

To simplify the description, I assume a projective geometry context. Thus I may speak of points at infinity and the line at infinity. Points at infinity occur as intersections of parallel lines and represent the slope of those lines. A point is at infinity if and only if it lies on the line at infinity.

To denote intersection of curves, I use the operator $\cap$ from set theory. Formally, this implies that the result of the intersection is not a point, but a set of points. Therefore intersection of distinct lines $\overline{AB}$ and $\overline{CD}$ in a point $P$ is written here as $\lbrace P\rbrace =\overline{AB}\cap\overline{CD}$.

Procedure

Knowing the foci implies knowing the symmetry axes of the conic. Therefore you can expect that finding foci is not easier than finding those symmetry axes. Consequently, finding foci usually includes the following steps:

1. Find the tangents to the conic at the given points.
2. Find the center.
3. Find the asymptotes, if those exist, and the lines containing the principal axes. Since the center is already known, only the respective slopes remain to be found.
4. Find the vertices.
5. Find the foci.
6. Find the directrices (while we are at it).

Finding the tangents

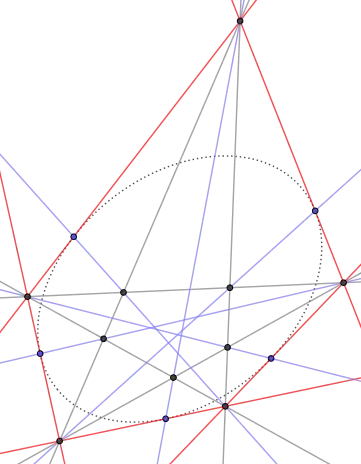
This is done using Pascal's theorem, pretending that one of the given five points is actually two infinitesimally close points on the conic, thus their joining line becomes a tangent to the conic. Constructing all five tangents this way can be illustrated with a nested-pentagram drawing as depicted below, with the resulting tangents colored red. This works for all types of conic sections. Bonus: This only needs a straightedge, unless points at infinity arise.

Just in case: The reverse can be done using a corresponding limit case of Brianchon's theorem, illustrated in the figure below.

Finding the center

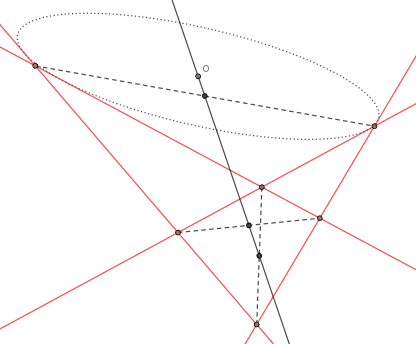
By intersecting diameters. Choose three of the given five points, say $A,B,C$, and construct a line $c$ through $C$ parallel to the line $\overline{AB}$. Then, using Pascal's theorem, construct the other point of intersection of $c$ with the conic, call it $C'$. Now we have parallel chords $[\overline{AB}]$ and $[\overline{CC'}]$. The line through their midpoints is known to pass through the center of the conic, therefore we call it a diameter. See the figure below. The solid black line is the diameter conjugate to the slope of the parallel blue lines. The construction shown is straightedge-only after having constructed the parallel line; it actually yields the polar of the point where the blue lines intersect. In this case, that point is at infinity, which implies that its polar passes through the center.

Repeat with different choices for $A,B,C$ such that $\overline{AB}$ changes slope; the intersection of the two diameters yields the conic's center.

Finding the center as intersection of polars of points at infinity means that we actually construct it as the pole of the line at infinity, which is a popular definition of a conic's center.

By intersecting Newton-Gauß lines. I prefer this one. Construct the five tangents first, then pick four of them. These form a complete quadrilateral. A complete quadrilateral has three diagonals, the midpoints of which are collinear. The containing line is known as Newton-Gauß line of the complete quadrilateral. It contains the centers of all conics with the given four tangents. This is illustrated below.

So, construct that Newton-Gauß line, then make another choice of four tangents out of the five given, and construct their Newton-Gauß line. Intersecting the two Newton-Gauß lines yields the conic's center.

By polar triangle pairs. Pick three of the given five points, say $A,B,C$, and the associated tangents $t_A,t_B,t_C$. Both $ABC$ and $t_At_Bt_C$ form triangles; let's call the vertices of the latter $A',B',C'$ such that $t_A=\overline{B'C'}$ etc. Now the triangles are in a polar relationship with respect to the conic: The polar of $A$ is $\overline{B'C'}$, the polar of $A'$ is $\overline{BC}$ etc. This implies that the triangles are perspective. In such a case, the center of the conic section is a fixed point of the affine transformation that takes $(A,B,C)$ to $(A',B',C')$. That fixed point can be constructed as the point of concurrence of the three lines $\overline{F_a F_A}$, $\overline{F_b F_B}$, $\overline{F_c F_C}$, where

$$\begin{aligned} \lbrace F_a\rbrace &= \overline{BC}\cap\overline{B'C'} &\lbrace F_A\rbrace &= (\overline{BC})_A\cap(\overline{B'C'})_{A'} \\\lbrace F_b\rbrace &= \overline{CA}\cap\overline{C'A'} &\lbrace F_B\rbrace &= (\overline{CA})_B\cap(\overline{C'A'})_{B'} \\\lbrace F_c\rbrace &= \overline{AB}\cap\overline{A'B'} &\lbrace F_C\rbrace &= (\overline{AB})_C\cap(\overline{A'B'})_{C'} \end{aligned}$$

Herein, $(\overline{BC})_A$ means the line through $A$ parallel to $\overline{BC}$. This is illustrated below.

This construction applies to the more general case where we are given three pole-polar pairs with respect to the conic, resulting in a pair of perspective triangles $(ABC, A'B'C')$, provided that $\overline{AB}\nparallel\overline{A'B'}$ etc to ensure that the lines $\overline{F_a F_A}$ etc are well defined and the fixed point is unique. Note that $F_a,F_b,F_c$ are collinear due to perspectivity, but the fixed-point construction does not require that.

For a case like this, with poles and polars being curve points and tangents, a simpler construction is available, cf. Intelligenti pauca's answer.

Parabolic case

If the conic is a parabola, all the above center constructions lead to an intersection of parallel lines, resulting in a point at infinity which indicates the slope of the parabola's symmetry axis, but nothing more.

Fortunately, the parabolic case is a bit simpler than the general case. A parabola has the line at infinity as a tangent, therefore it is already determined by four other tangents.

Pick three tangents and have them form a triangle $A'B'C'$. The focus of the parabola must lie on the circumcircle of $A'B'C'$ (that's Lambert's theorem), and its directrix must pass through the orthocenter of the triangle $A'B'C'$ (that's some theorem by Steiner, if I recall correctly). The availability of more than three tangents allows us to use more triangles, and this suffices to determine both focus and directrix uniquely.

You could as well focus on finding the focus first, then mirror that focus across the available tangents. All mirror images lie on the directrix.

(In the non-parabolic case, the mirror images of a focus would lie on a circle whose center is the other focus.)

Finally, the parabola's vertex is halfway between the focus and the directrix.

Note: When determining a parabola from four tangents, it is tempting to assume that the associated Newton-Gauß line is the parabola's symmetry axis and therefore contains the focus. That is usually not the case. What we know is that the Newton-Gauß line is parallel to the parabola's symmetry axis. In the language of projective geometry, those two lines still intersect in the parabola's center, but that is a point at infinity.

Finding symmetry axes and asymptotes, if any

Back to the general case. We already have the center, so we just need to find lines with the slopes of the desired axes or asymptotes, then parallel-shift those lines such that they pass through the center.

The main trick to find the interesting slopes from given five points is isogonal conjugation, also used in my answer to a related question. Pick three of the given five points, say $A,B,C$ and use these as reference triangle. Generally, the isogonal conjugate $P'$ of a point $P\not\in\lbrace A,B,C\rbrace$ is the point of concurrence of the lines $(\overline{AP})^{\angle CAB}$, $(\overline{BP})^{\angle ABC}$ and $(\overline{CP})^{\angle BCA}$. Here, $(\overline{AP})^{\angle CAB}$ means mirroring the line $\overline{AP}$ across the angle bisector of $\angle CAB$. The inverse transform is again isogonal conjugation.

Note that the conic is a circumconic of $ABC$. Construct the isogonal conjugates $D',E'$ of the remaining two points $D,E$. Now the line $\overline{D'E'}$ contains the isogonal conjugates of all points of the conic (if we define image points of $A,B,C$ by continuity along the conic). In a sense, we have morphed the conic into a line.

There are other operations beside isogonal conjugation that can morph a conic into a projective line, but isogonal conjugation has an additional useful feature, which is as follows.

Let $u$ denote the circumcircle of $ABC$. Isogonal conjugation turns points on $u$ into points at infinity (if we remove singularities at $A,B,C$ suitably) and vice versa. This leads to the following observations:

• If both $D'$ and $E'$ are points at infinity, then $\overline{D'E'}$ is the line at infinity, and the conic is the circle $u$ itself. The following considerations assume that this is not the case.

• If the line $\overline{D'E'}$ intersects $u$, then the points of intersection $P_1',P_2'$ are the isogonal conjugates of the points at infinity $P_1,P_2$ that belong to the conic. This implies that the conic is a hyperbola (or a parabola if $P_1=P_2$), and $P_1,P_2$ represent the slopes of its asymptotes (or the slope of the symmetry axis of the parabola).

  $P_1,P_2$ can be obtained as isogonal conjugates of $P_1',P_2'$. When breaking this down to more elementary steps, each $P_i$ will arise as intersection of parallel lines. Since we only need to know the associated slope, we are done as soon as we have constructed one of those lines. Concretely, if $P_i'\neq A$, we can mirror $\overline{AP_i'}$ across the angle bisector of $\angle CAB$; the resulting line has the sought slope.

• If there are no points of intersection $P_i'$, then the conic is an ellipse.

• The slope of the line $\overline{D'E'}$ determines the slopes of the principal axes of the conic. To see why, consider the point at infinity of $\overline{D'E'}$. Let us name it $K'$. It must be the isogonal conjugate of a point $K$ both on the conic and on $u$, therefore $A,B,C,K$ are concyclic. The family of conics through $A,B,C,K$ is a pencil of conics; the associated quadratic forms are linear combinations of the quadratic forms of two of its member conics. One of the forms can be chosen to be the circle $u$. However, combining a quadratic form with a circle form does not change the slopes of the associated principal axes. Therefore, all conics through concyclic $A,B,C,K$ share a common pair of slopes for their principal axes. Isogonal conjugation turns the conics in that pencil into lines parallel to $\overline{D'E'}$ (formally, a pencil of lines through the point at infinity $K'$).

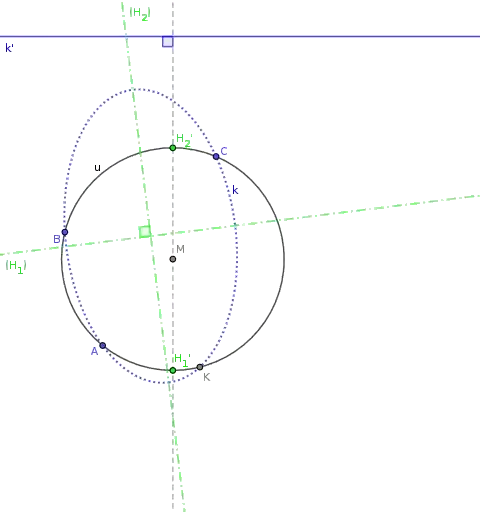
  We do not even need to construct $K$. Instead, consider the two lines $h_1',h_2'$ parallel to $\overline{D'E'}$ that just touch $u$, and name the points of tangency $H_1',H_2'$. Isogonal conjugation yields $H_1,H_2$ which are the points at infinity of the two parabolas through $A,B,C,K$. For those, $H_1,H_2$ represent slopes of principal axes, and those apply to all conics in the pencil, including our conic.

  Geometrically, $H_1', H_2'$ are the points of intersection of the line $r$ with $u$, where $r$ is the line orthogonal to $\overline{D'E'}$ that passes through the center of $u$.

  Sanity check: $H_1',H_2'$ are antipodes on $u$. By Thales's theorem, $\overline{AH_1'}$ and $\overline{AH_2'}$ are orthogonal, as are $(\overline{AH_1'})^{\angle CAB}$ and $(\overline{AH_2'})^{\angle CAB}$. Therefore the slopes represented by $H_1,H_2$ turn out to be orthogonal, as they should be.

Sidenote: With isogonal conjugation, it is easy to prove that a circumconic of a non-right-angled triangle is a rectangular hyperbola if and only if the circumconic also passes through the triangle's orthocenter.

Finding the vertices

From here onward, we assume that the conic is neither a circle nor a parabola, so it has a finite center $O$ and two orthogonal symmetry axes, both of which are known by now. Concretely, with $H\in\lbrace H_1,H_2\rbrace$ denoting a point at infinity representing the slope of one of the principal axes, the associated symmetry axis is $\overline{OH}$ and can be constructed e.g. by parallel-shifting $\overline{AH}$ (which occurs when isogonally conjugating the associated $H'$ on $u$).

To find the vertices on $\overline{OH}$ (if any), pick one of the given points on the conic, say $A$, and its associated tangent $t_A$. Mirroring $A$ across $\overline{OH}$ yields another point $A'$ on the conic. Imagine mirroring the tangent $t_A$ to $t_{A'}$ as well. Set $\lbrace P\rbrace = t_A\cap t_{A'} = t_A\cap\overline{OH}$ and $\lbrace Q\rbrace = \overline{AA'}\cap\overline{OH}$. Now $p=\overline{AA'}$ is the polar associated with the point $P$, which implies that $P,Q$ and the two vertices $V_{1,2}$ on $\overline{OH}$ form a harmonic range. Those vertices exist (as real points) if and only if the center $O$ is outside the segment $[\overline{PQ}]$, otherwise we have a hyperbola and $\overline{OH}$ contains the minor axis and no (real) vertices.

Assuming that $O$ is outside the segment $[\overline{PQ}]$, the harmonic-range property implies that

$$\left\vert OP\right\vert\cdot\left\vert OQ\right\vert = \left\vert OV_{1,2}\right\vert^2$$

Therefore we can find $V_{1,2}$ with a geometric-mean construction. Here is one of those: Construct a Thales circle $s$ on $[\overline{PQ}]$, call its center $S$. Construct a Thales circle on $[\overline{OS}]$, intersecting $s$ in the points $S_{1,2}$. Draw a circle around $O$ through $S_{1,2}$; this one intersects $\overline{OP}$ in $V_{1,2}$.

Note that this construction works not only along a symmetry axis; actually it works for any pole-polar pair $(P,p)$ with $\lbrace Q\rbrace = p\cap\overline{OP}$, as long as $O\not\in[\overline{PQ}]$. It yields the points of intersection of $\overline{OP}$ with the conic, provided that $O$ is their midpoint. This is illustrated below.

Finding the foci

From major vertices and one tangent: Herein, vertices are considered to be major (resp. minor) if the conic has maximal (resp. minimal) curvature there. An ellipse also has minor vertices, but the method presented here does not need those and works for hyperbolas as well.

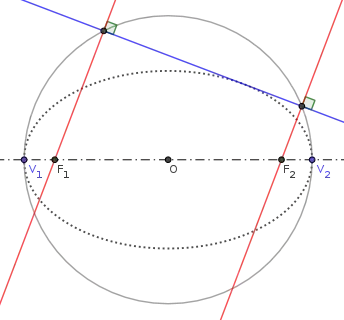
Draw the major vertex circle around the conic's center $O$, passing through the major vertices. Now pick any tangent that does not pass through a major vertex. That tangent has to intersect the major vertex circle in two points $P_1,P_2$. Draw perpendiculars $p_1,p_2$ to the tangent through those points. Then $p_1,p_2$ intersect the major axis in the foci.

Getting the perpendiculars does not need a compass because we can simply draw the lines $\overline{OP_{1,2}}$, and their four points of intersection with the major vertex circle (including $P_{1,2}$) form a rectangle.

This method essentially tells us that the pedal point of a focus on a tangent always lies on the major vertex circle. Imagine the pedal point and the major vertex circle scaled away from the focus with a factor of 2, and you get the perhaps more familiar statement that mirroring a focus across a tangent yields a point whose distance to the other focus equals the distance between the major vertices.

From three tangents and the major vertex circle: We could generalize the previous approach to only need the major vertex circle, but not the major axis, as long as we also have three pairwise nonparallel tangents available.

The major vertex circle has to intersect the given three tangents in $3\times2$ points (counted with multiplicity). Draw perpendiculars to the intersected tangents there. There will be two points $F_1,F_2$, symmetric around $O$, where three of these perpendiculars meet. Those are the foci. This is illustrated below.

As before, if you have the circle and its center $O$ drawn already, the perpendiculars can be constructed with straightedge only.

One practical problem with this method is that it requires exactness. If you get the major vertex circle radius wrong by a tiny amount, then there will be no three concurrent perpendiculars.

The other obvious drawback is that you need the major vertex circle. Determining that with the methods outlined above requires finding vertices, which requires finding symmetry axes in turn. Therefore this approach does not actually save work.

Finding the directrix associated with a focus

The directrix is the polar of the focus, both with respect to the major vertex circle and with respect to the conic itself. This means that we can use a straightedge-only polar construction method once the major vertex circle has been drawn.

As a consequence of that polar relationship, the point of intersection of the directrix with the major axis is the image of the focus from inversion with respect to the major vertex circle.

Answer 2

Given five points of the conic, and using Pascal's theorem you are able to find the intersection of the conic with an arbitrary line that contains one of these. Moreover, you are able to find the tangent to the conic at any of these points.

Now, you are able to produce pairs of conjugate diameters that intersect at the center of the conic (ellipse). To do that, notice that the middle of the chords parallel to a given direction are all on the line passing through the center of the ellipse (the conjugate diameter). This produces conjugate directions, to get the sizes of the diameters one uses Prop XXII from the source below. Up to now, we haven't mentioned angles.

The rest, and most interesting part is explained in an old book that you can find here: An elementary treatise on the Geometry of Conics, page 96, ex 8. There îs one beautiful basic fact being used , that the product of the intercepts on the tangent to an ellipse by a pair of conjugate directions is constant (equals the square of the half the diameter parallel to the tangent). With this and some classical construction one is able (ex 8 mentioned above) to construct a pair of conjugate directions that are perpendicular, so the axes. One now uses a consequence of prop XXII in the same book to get the sizes of the diameters.

I noticed now that one can also use results from page 106 of the same book (ex 14 or 15).

Also see Rytz's construction.

All these results seem classical, to be known by Newton and maybe even before him (Apollonius?), but forgotten these days, since the geometry of conics is nowadays seen as a particular case of "analytic geometry", excepts perhaps the "fun things" like Pascal, Brianchon, Poncelet and very basic things.

Answer 3

Given just 5 points that are known to lie on the perimeter of an ellipse, and generating that ellipse using the method described in the partial answer offered here by @Ng, and then continuing with the instructions found at http://whistleralley.com/conics/conic_construction/ellipse_parts/, it is possible to construct the entire ellipse, its major and minor axes, center, vertices, foci, and directrices. Therefore, this is a valid solution to my question as posed, however the initial construction of the ellipse still requires using more than just a compass and straight edge, so I am still hoping for a ruler-and-compass only solution. Thanks again @Ng for supplying the first steps that I was missing.

Answer 4

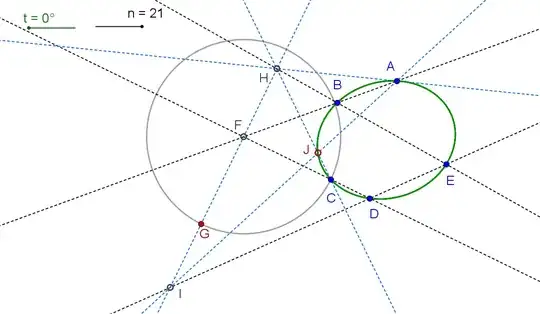
Point $G$ is a dynamic point on circle containing $C$.

Point $J$ forms a locus of the conic containing $A$, $B$, $C$, $D$ and $E$.