In smls's post "Find the properties of an ellipse from 5 points in 3D space" (Find the properties of an ellipse from 5 points in 3D space), Intelligenti pauca presented a pure geometrical answer. I tested that method and found it good. But I cannot prove the process of finding the tangent A-TA. Anyone can show me the proof?
-
1It was better to post a comment to that solution asking for a proof: I would have added it to my answer. – Intelligenti pauca Sep 16 '20 at 10:56
1 Answers
That trick is based on Pascal's Theorem:
If six arbitrary points are chosen on a conic (which may be an ellipse, parabola or hyperbola) and joined by line segments in any order to form a hexagon, then the three pairs of opposite sides of the hexagon (extended if necessary) meet at three points which lie on a straight line, called the Pascal line of the hexagon.
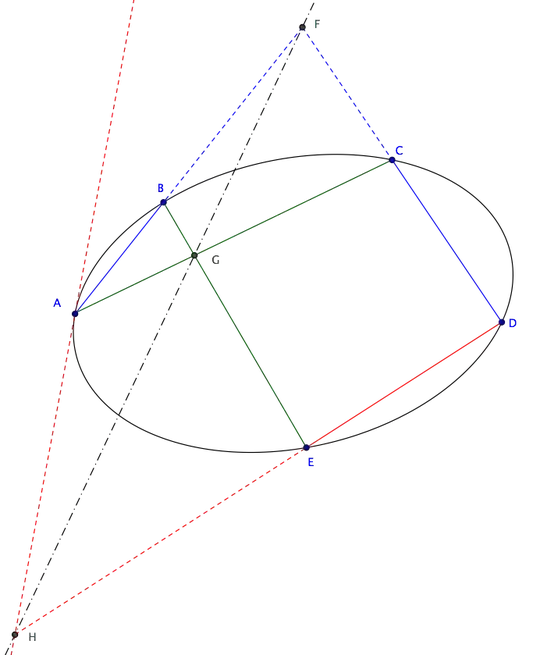
You can see the theorem at work in the figure below: hexagon $A'ABEDC$ is inscribed in an ellipse and its three pairs of opposite sides (having the same colour in the figure) meet at points $F$ (intersection of $AB$ and $CD$), $G$ (intersection of $A'C$ and $BE$) and $H$ (intersection of $A'A$ and $DE$), which lie then on the same line.
Suppose now you let $A'$ approach $A$ closer and closer: in the limit $A'\to A$ line $AA'$ becomes the line tangent to the ellipse at $A$ (see second figure).
This gives a method to construct the tangent at $A$ to a conic passing through points $ABCDE$: it is the line through $A$ and $H$, the latter being the intersection point of lines $FG$ and $DE$. Points $F$ and $G$ are constructed as explained above but with $A'$ replaced by $A$: $F$ is the intersection of $AB$ and $CD$, $G$ is the intersection of $AC$ and $BE$.
- 50,470
- 4
- 42
- 77
-
I cannot see the figures you placed. Could u please email them to me [email protected]? – fosuwxb Sep 16 '20 at 14:35
-
@fosuwxb I'd prefer not to send emails. I could post them somewhere else, where you can see them, if you let me know the address. – Intelligenti pauca Sep 16 '20 at 14:50
-
@fosuwxb On the other hand you can easily reconstruct the figures: points $A'ABCDE$ are taken clockwise on the ellipse in that order. – Intelligenti pauca Sep 16 '20 at 15:59
-
A'C and BE are opposite sides? Because I cannot see the figures, I am not sure the meaning of the opposite ones. Could U please have some way to show them? what kind of browsers can see the figures? – fosuwxb Sep 17 '20 at 21:49
-
1Yes, they are opposite sides. That's because the points $A'ABCDE$ lie on the ellipse in that order, clockwise, but the hexagon of Pascal's theorem is formed by points $′$ in that order. That's only a matter of convenience, to get points $F$ and $G$ not too far in the figure: the reasoning would work for any choice of hexagon. Moreover, bear in mind that two opposite sides could also be parallel: in that case they meet at a point at infinity. – Intelligenti pauca Sep 18 '20 at 06:57