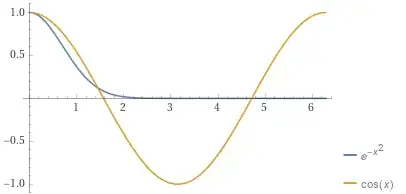
How to prove that $\displaystyle I=\int_0^{2\pi}e^{-x^2}\cos(x)\mathrm{d}x>0$
Clearly, $\displaystyle I=\int_0^\pi \left(e^{-x^2}-e^{-(x+\pi)^2}\right)\cos(x)\mathrm{d}x$, but this does not help.
Or else, $$I=\int_0^{2\pi} e^{-x^2}\mathrm{d}\sin(x) =2\int_0^{2\pi} xe^{-x^2}\sin(x)\mathrm{d}x =2\int_0^\pi \left(xe^{-x^2}-(x+\pi)e^{-(x+\pi)^2}\right)\sin(x)\mathrm{d}x.$$ This time, $\sin(x)$ has a good sign, but $xe^{-x^2}$ has no monotonicity property.
Any ideas?
Use the inequality $\cos x\ge 1-\frac{x^2}2$ to write: $$ \int_0^{2\pi}e^{-x^2}\cos x\,{\rm d}x\ge\int_0^{2\pi}\left( e^{-x^2}-\frac{x^2}2 e^{-x^2}\right)\,{\rm d}x=A - B.$$ To show $A>B$, compute a lower bound for $A$ using the inequality $e^{-t}\ge 1-t$: $$A:=\int_0^{2\pi}e^{-x^2}\,{\rm d}x\ge\int_0^1 e^{-x^2}\,{\rm d}x\ge\int_0^1\left(1- x^2\right)\,{\rm d}x=\frac23.$$ Find an upper bound for $B$ using the fact $\int_0^\infty x^2e^{-x^2}\,{\rm d}x=\frac{\sqrt\pi}4$: $$B:=\frac12\int_0^{2\pi}x^2e^{-x^2}\,{\rm d}x\le\frac12\int_0^\infty x^2e^{-x^2}\,{\rm d}x=\frac{\sqrt\pi}8.$$
This approach also proves the non-trivial case ($t>\frac\pi2$) for the general result $$ \int_0^t e^{-x^2}\cos x\,{\rm d}x>0\qquad\text {for all $t>0$}. $$
The integral $I_1=\int_0^{\pi/2}f(x)\,dx$ is positive (as the integrand is positive in this interval) and $$I_1>\int_0^{\pi/4}f(x)\,dx>\frac{\pi}{4}\cdot \frac{e^{-\pi^2/16}}{\sqrt{2}}\tag{1}$$ as the integrand is decreasing in this interval and hence greater than $f(\pi/4)$.
Further $I_2=\int_{\pi/2}^{3\pi/2}f(x)\,dx$ is negative with $$|I_2|\leq \int_{\pi/2}^{3\pi/2}|f(x)|\,dx<\pi \cdot e^{-\pi^2/4}\tag{2}$$ and our job is done if we can show that RHS of $(1)$ is greater than that of $(2)$.
This requires us to prove that $e^{3\pi^2/16}>4\sqrt {2}$ or $$\frac{3\pi^2}{8}>5\log 2$$ This is possible by noting that $\log 2<0.7$ and $\pi>3.14$.
Bounds for the integral on subintervals: $[0,\pi/4]: I_{11}>\frac1{\sqrt2}e^{-\pi^2/16}\\ [\pi/4,\pi/2]: I_{12}>(1-\frac1{\sqrt2})e^{-\pi^2/4}\\ [\pi/2,\pi]: I_{2}>-e^{-\pi^2/4}\\ [\pi,3\pi/2]: I_{3}>-e^{-\pi^2}\\ [3\pi/2,2\pi]: I_{4}>e^{-4\pi^2}\\ $
Adding these we have $$I=\int_0^{2\pi}e^{-x^2}\cos x\, dx>\frac1{\sqrt2}(e^{-\pi^2/16}-e^{-\pi^2/4})-e^{-\pi^2}> \frac1{\sqrt2}(e^{-0.64}-e^{-9/4})-e^{-9}>0. $$
The integral is the area under the curve.
The product of $e^{-x^2}$ and $\cos(x)$ is mostly positive in the interval given for x . Think of it pointwise, at every x in the interval. You may split the integral into the negative and positive area parts of $\cos(x)$ since the $e^{-x^2}$ Gaussian function is positive and compare or bound those pieces for a formal proof.
