Can someone help me prove that $0 \leq 1 -\cos(x) \leq x^2/2$
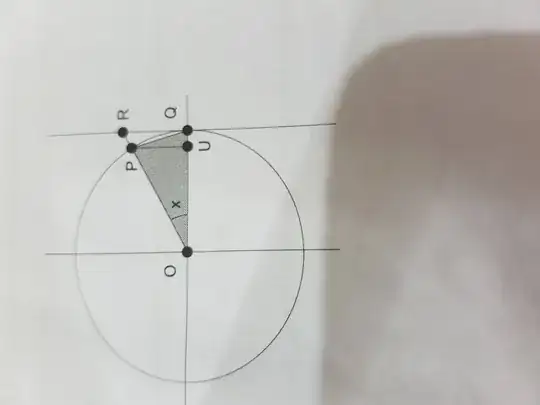
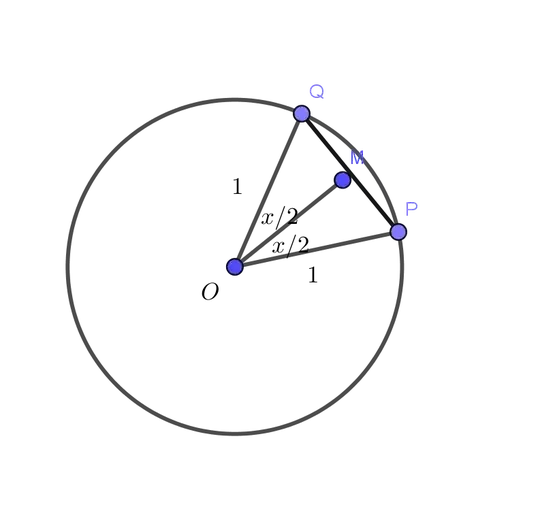
The hint from the book, was that I could assume that $ x \in (0, PI/2), $ then I could use Pythagoras' to realise that $ |QP| = \sqrt(2 -2cosx)$ and use that the line QP must be shorter than the arc lenght between the two points. And from there I can use the same arguemnt for $ x \in (Pi/2, PI)$. But I don't quite understand what to do.