Shortest distance from point to a curve and Estimation of error of an incorrect approach

Question

Today I wrote an answer to a question in regards to the topic of shortest distance between a point and a curve, more precisely an ellipse, check here. Turns out the answer was incorrect, yet it was a close approximation, so it sparked an interesting discussion in the comments.

TLDR
My logic for finding a shortest distance from a specific point to an ellipse was to find tangent lines from that point to an ellipse and from there to find a line of symmetry of those two lines. That line of symmetry would intersect the ellipse and would be perpendicular to it, meaning that it should have given me the correct distance. Instead I got an estimate that was accurate up to the third decimal (might be because of rounding up because later when I checked with more decimal points it was incorrect at the second decimal).

For some backstory, I'm not sure how I got this idea. I've seen it used a few times with a circle (couldn't give you any examples right now) so I thought, using similar logic, that the same could be applied to an ellipse, but I guess I should of proved it beforehand.

Let's take a look at the logic I used. I will visualize things for easier understanding.

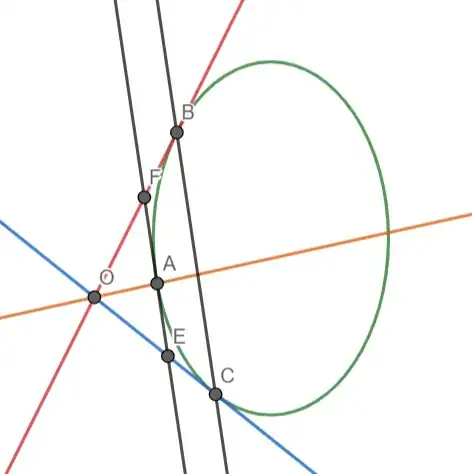
In the following text, I'll bold possibly incorrect statements. As you can see in the drawn out image, from point $O$ there are two tangent lines, let's denote them as $t_1, t_2$, to an ellipse that touch it at points $B$ and $C$, respectively. Then there is a line of symmetry between the lines $t_1$ and $t_2$, we'll call it $s$. Similarly to the circle the, we can say that $\pmb{\overline{OB}=\overline{OC}}$, meaning $\pmb{\triangle{OBC}}$ is isosceles. Now let's draw a line parallel to the one passing through $B$ and $C$ such that it passes through point $A$ and it is tangent of an ellipse (this is the most questionable statement). Now since all the lines of a triangle $\triangle OEF$ and $\triangle OBC$ are parallel it means they are similar, as such $\pmb{\triangle OEF}$ is isosceles. Because $s$ is a line of symmetry between two lines defined by two sides of $\triangle OEF$, it means that $s$ is line of symmetry of $\angle OEF$, from the fact that it is isosceles triangle, we can conclude that $\pmb{\overline{OA}}$ is the height of $\pmb{\triangle OEF}$. As such, we can say that it is perpendicular to the tangent of an ellipse passing through $\pmb A$.

You can see that all of the bolded points were directly related to one of two:
$1.$ $\overline{OB}=\overline{OC}$,
$2.$ Line parallel to the one passing through $B$ and $C$ such that it passes through point $A$ is tangent of an ellipse.

My question is if you could prove or disprove both or any of these two statements (for example prove the correct one and disprove the incorrect one) which most likely led me to a mistake.

Note
I know it is very likely that at least one of those statements is incorrect, so if you were to disprove them could you do like a general case, because I've already seen it on a specific example, I'm of course talking about the one in the original post I've answered to.

Another thing I'd like to ask, in the comments user Ennar raised a good concern, basically asking about the error estimate of doing the calculation of the question the way I did it. Is there any general formula for that estimate that could be found?

Another Note
I know this specific example used an ellipse, but it could of course be applied to any curve with the exception of circle because we know that shortest distance from point to a circle could be found with the mentioned method.

Edit
Based on one of my comments here, user mathlove has given an answer. Essentially finding the angle $\angle AOA_1$, where $O$ and $A$ are like in the picture I've posted and $A_1$ is the point that is the real closest point on the curve (in this case an ellipse) to $O$. My idea was that function of error of my estimation can be represented as a function of that angle $\angle AOA_1$. After we find the angle how to do the rest of the job, how to relate it to the precentage error from the correct answer? After writing the comment about this idea for finding function for error I thought maybe it wasn't the best idea. Especially considering how you would already need to know the correct answer to find the error, but then there is no need in finding one if you already have the correct solution.
That's just me thinking out loud. Any ideas and suggestions will be appreciated.

Answer 1

To disprove the first statement:

Take the tangents that are parallel to the long and short axes of the ellipse. They intersect to a point (O) that is not at equal distance to the contact points B and C of the tangents with the ellipse. So OB ≠ OC.

Answer 2

Take the circle $x^2 + y^2 = 1$. It is bound by axis-aligned square that goes through $(-1;1),(1;1),(1;-1),(-1;-1)$ points.
Take one of those points, let's say $O = (-1;1)$ - upper left corner.
From your solution, $B = (0;1), C = (-1;0)$

Now we stretch the picture in x-direction. Circle becomes an ellipse $(Nx)^2 + y^2 = 1$.
The point $O$ becomes $(-N;1)$.
Tangent lines are parallel or perpendicular to the stretch, so they don't change. $B = (0;1), C = (-N;0)$

Already here you can see that $OB \ne OC$ by an arbitrary amount.

Real closest point would be within 1 unit from $O$, since $C$ is part of ellipse at that distance.
But as we increase $N$, $BC$ becomes more horizontal, so $A$ moves further and further away.

Here's geogebra of roughly this situation

Answer 3

You said in a comment that

let's denote the point of intersection of line of symmetry and curve as $A$ and extremal point of the curve as $A_1$. Would that mean that the error function could be represented in sume way as a function of $\angle{A_1OA}$ ?

Let us consider two tangent lines $OB,OC$ where $B,C$ are tangent points on the curve $\dfrac{(x-c)^2}{a^2}+\dfrac{(y-d)^2}{b^2}=1$ with $a>0$ and $b>0$.

First, let us find the slope $M_1$ of the line $OA$.

Letting $y=mx$, we get $\dfrac{(x-c)^2}{a^2}+\dfrac{(mx-d)^2}{b^2}=1$, i.e. $$(b^2+a^2m^2)x^2-2(b^2c+a^2md)x+b^2c^2+a^2d^2-a^2b^2=0$$

Now, $D=0$ is equivalent to $$4(b^2c+a^2md)^2-4(b^2+a^2m^2)(b^2c^2+a^2d^2-a^2b^2)=0$$ i.e. $$(a^2-c^2)m^2+2cdm+b^2-d^2=0$$

If $a^2-c^2\not=0$, then letting $m_1,m_2$ be the roots, we have $$m_1+m_2=-\frac{2cd}{a^2-c^2},\qquad m_1m_2=\frac{b^2-d^2}{a^2-c^2}$$

Therefore, the equation of the line $OA$ is given by one of $$\frac{m_1x-y}{\sqrt{m_1^2+1}}=\pm\frac{m_2x-y}{\sqrt{m_2^2+1}}$$ So, $M_1$ is one of $$\begin{align}&\frac{\pm m_2\sqrt{m_1^2+1}-m_1\sqrt{m_2^2+1}}{-\sqrt{m_2^2+1}\pm\sqrt{m_1^2+1}} \\\\&=\frac{(\pm m_2\sqrt{m_1^2+1}-m_1\sqrt{m_2^2+1})(-\sqrt{m_2^2+1}\mp\sqrt{m_1^2+1})}{(-\sqrt{m_2^2+1}\pm\sqrt{m_1^2+1})(-\sqrt{m_2^2+1}\mp\sqrt{m_1^2+1})} \\\\&=\frac{\mp\sqrt{(m_1^2+1)(m_2^2+1)}-1+m_1m_2}{m_1+m_2} \\\\&=\frac{\mp\sqrt{(\frac{b^2-d^2}{a^2-c^2})^2+(-\frac{2cd}{a^2-c^2})^2-2(\frac{b^2-d^2}{a^2-c^2})+1}-1+\frac{b^2-d^2}{a^2-c^2}}{-\frac{2cd}{a^2-c^2}} \\\\&=\frac{\pm\sqrt{(a^2-b^2-c^2+d^2)^2+4c^2d^2}+a^2-c^2-b^2+d^2}{2cd}\end{align}$$ We get $$M_1=\frac{\color{red}+\sqrt{(a^2-b^2-c^2+d^2)^2+4c^2d^2}+a^2-c^2-b^2+d^2}{2cd}$$ since $M_1$ has to satisfy $(a^2-c^2)M_1^2+2cdM_1+b^2-d^2\gt 0$.)

---

Next, let us consider the slope $M_2$ of the line $OA_1$.

Let us use this answer. Our curve is $\dfrac{(x-c)^2}{a^2}+\dfrac{(y-d)^2}{b^2}=1$, so we get the system $\begin{cases}2x=\frac{2(x-c)\lambda}{a^2} \\2y=\frac{2(y-d)\lambda}{b^2}\end{cases}$, so eliminating $\lambda$ gives $y=\dfrac{a^2dx}{(a^2-b^2)x+b^2c}$, so we finally get

$$(a-b)^2(a+b)^2x^4-2 c (a - b) (a + b) (a^2 - 2 b^2)x^3+(-a^6+ 2 a^4 b^2 + a^4 c^2- 6 a^2 b^2 c^2+ a^2 b^2 d^2 + 6 b^4 c^2 - a^2 b^4 )x^2-2 b^2 c (a^4 - a^2 b^2 - a^2 c^2 + a^2 d^2 + 2 b^2 c^2)x+b^2 c^2 (-a^2 b^2 + a^2 d^2 + b^2 c^2)=0\tag2$$

Let $X$ be the $x$-coordinate of $A_1$. Then, $X$ is a root of $(2)$.

Then, the slope of the line $OA_1$ is given by $M_2=\dfrac{a^2d}{(a^2-b^2)X+b^2c}$.

$\angle{A_1OA}$ can be represented as $$\angle{A_1OA}=\arctan\bigg(\frac{M_1-M_2}{1+M_1M_2}\bigg)$$

---

Example : $a=3,b=4,c=2,d=5$

We get $M_1=\dfrac{7+\sqrt{149}}{10}$, and $(2)$ has two real roots $x\approx 0.7888, 2.6547$. The former is what we want, and so $M_2\approx 1.3596$.

So, we get $\color{red}{\angle{A_1OA}\approx 8.831^\circ}$.

Answer 4

The problem can be reformulated as concurrent normals through a given point.

• A central conic has $2$ to $4$ concurrent normals from a given point.

• A parabola has $1$ to $3$ concurrent normals from a given point.

• For a conic $S$ in general form

$$0= \begin{pmatrix} x & y & 1 \end{pmatrix} \begin{pmatrix} a & h & g \\ h & b & f \\ g & f & c \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \tag{1}$$

• Equation of tangent at $(X,Y)$ lying on $S$

$$0= \begin{pmatrix} X & Y & 1 \end{pmatrix} \begin{pmatrix} a & h & g \\ h & b & f \\ g & f & c \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} \tag{2}$$

• Equation of normal at $(X,Y)$ lying on $S$

$$0= \begin{pmatrix} X & Y & 1 \end{pmatrix} \begin{pmatrix} a & h \\ h & b \\ g & f \end{pmatrix} \begin{pmatrix} y-Y \\ X-x \end{pmatrix} \tag{3}$$

• If $B$, $C$, $D$ and $E$ are the feet (or pedals) of the concurrent normals from $A(x',y')$, then switching the roles of $(x,y)$ and $(X,Y)$ gives an Apollonian rectangular hyperbola

$$0= \begin{pmatrix} x & y & 1 \end{pmatrix} \begin{pmatrix} a & h \\ h & b \\ g & f \end{pmatrix} \begin{pmatrix} y'-y \\ x-x' \end{pmatrix} \tag{4}$$

• The intersections of two conics are the required feet of the concurrent normals.

• The rectangular hyperbola also passes the centre of a central conic.

• Up to first order, a very rough approximate of the closest pedal is

$$ \begin{pmatrix} x' \\ y' \end{pmatrix}- \frac{ \begin{pmatrix} x' & y' & 1 \end{pmatrix} \begin{pmatrix} a & h & g \\ h & b & f \\ g & f & c \end{pmatrix} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} }{2 \begin{Vmatrix} \begin{pmatrix} a & h & g \\ h & b & f \end{pmatrix} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} \end{Vmatrix}^{\,2}} \begin{pmatrix} a & h & f \\ h & b & g \\ \end{pmatrix} \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix}$$

• For further interests, please refer to older posts of mine here and here.

Useful fact:

Equation of tangent for a conic $ax^2+2hxy+by^2+2gx+2fy+c=0$ at the point $(x',y')$ is given by

$$ax'x+h(y'x+x'y)+by'y+g(x+x')+f(y+y')+c=0$$

Answer 5

As an extreme numerical counter example take the case of one thinnest allowable ellipse whose ends of major axis are situated at $(0,3), (5,12). $ Center is at $(2.5,4.5);~~ 2a= \sqrt{5^2+9^2},~ 2b=0; $

Tangent lengths $(3, 13) $ are not equal.