$P$ is a point in $\triangle ABC$, with $\angle PBC=\angle PCB=24^\circ$, $\angle ABP=30^\circ$, $\angle ACP=54^\circ$. What is the $\angle BAP$?

Question

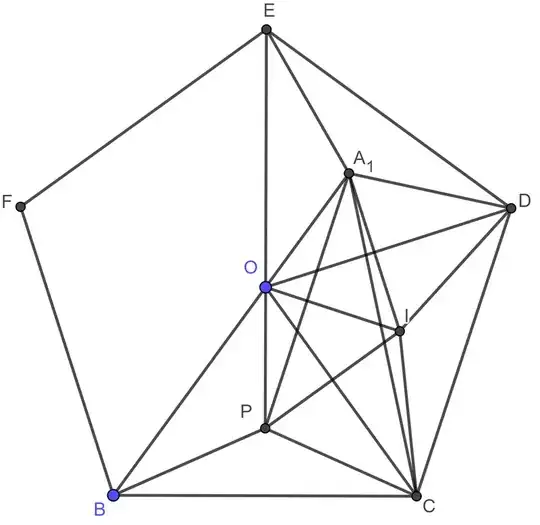
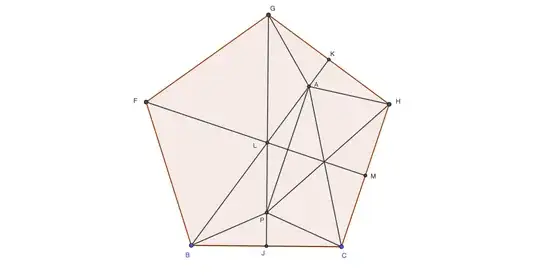
Let $P$ be a point inside a triangle $\triangle ABC$ with $\angle PBC=\angle PCB=24^\circ$, $\angle ABP=30^\circ$ and $\angle ACP=54^\circ$. What is the $\angle BAP$?

I can calculate $\angle BAP=18^\circ$ by assuming $BC=1$ and calculating all the lengths involved in the picture using formula of sines and cosines.

But since the answer is an integer $18^\circ$, I believe there must be a more elementary ways (i.e. without using sines/cosines or invloving irrational numbers) to obtain the answers.

Any suggestions are welcome! Thank you in advance!

Answer 1

1. Let $Q$ on $AB$ such that $PQ \cong PB \cong PC$.
2. By angle chasing, $\measuredangle QPC = 108^\circ$. Hence we can construct the regular pentagon $PQRSC$ shown above, where, in particular, $AC$ perpendicularly bisects $QR$.
3. $\triangle AQR$ is isosceles, and angle chasing yields $\measuredangle AQR = 42^\circ$.
4. Let now $A'$ on $CA$ (on the same side as $A$, with respect to $PS$) such that $\triangle PA'S$ is equilateral. We will show that $A' \equiv A$. We have in fact that $\triangle A'QS$ is isosceles, and angle chasing gives $\measuredangle A'SQ = 24^\circ$. Hence $\measuredangle A'QS = 78^\circ$, $\measuredangle A'QR = 42^\circ$, and by 3. we have our conclusion.
5. So $\measuredangle PAS = 60^\circ$, that is $\measuredangle PAC = 30^\circ$, hence the result $$\boxed{\measuredangle BAP = 18^\circ}.$$

Answer 2

Let draw regular pentagon BCDEF with center O. Let P is point such that $\angle PBC=\angle PCB=24$°, I is point such that $\angle ICD=\angle IDC=24$°, A$_1$ is point such that $\angle A_1DE=\angle A_1ED=24$°. Triangles PIC and A$_1$ID are regular and equal. Then triangle $A_1IC$ is isosceles with $\angle A_1IC=360$°$-60$°$-132$°$=168$°, then $\angle ICA_1=6$°, $\angle PCA_1=54$°.

A$_1$, O and B lie on perpendicular bisector of the edge DE, then $\angle A_1BP=\angle OBP=30$°. Then A$_1$ is the same point as A from problem statement. Then $\angle BAP=\angle OA_1P=18$°

Answer 3

Here is a great party, so i will join. The point $\Omega$ below also shows up in many other solutions, but somehow i missed a quick argument.

---

Construct on $BP$ and $CP$ two equilateral triangles $\Delta BPQ$ and $\Delta CPT$ as in the picture. The perpendicular bisectors of $PQ$ (which also passes through $A,B$) and of $PT$ intersect in a point, call it $\color{blue}\Omega$, which also lies on the perpendicular bisector of $BC$. We obtain now by symmetries $\color{blue}\Omega Q=\color{blue}\Omega P=\color{blue}\Omega T$, and $\Delta \color{blue}\Omega BC$ isosceles, so we know the angles: $$ \widehat{Q\color{blue}\Omega P}= \widehat{P\color{blue}\Omega T}=72^\circ\ . $$

This means that we can extend the broken line $TPQ$ to a regular pentagon $TPQRS$, with center of symmetry in $\color{blue}\Omega$ as in the picture. The marked angle in $T$ in the isosceles $\Delta TSC$ is $60^\circ+108^\circ$, so $\widehat {TCS}=6^\circ$, giving $\widehat {SCP}=60^\circ-6^\circ=54^\circ=\widehat {ACP}$. The point $S$ is thus $S=B\color{blue}\Omega A \cap CA=A$. Finally: $$ x=\widehat{BSP}=\widehat{\color{blue}\Omega SP}= \frac 12\widehat{QSP}=\frac 12\cdot 36^\circ=\bbox[yellow]{\ 18^\circ \ }\ . $$

Answer 4

I'm a 9th grader in Viet Nam so my English won't be too good. Sorry for this inconvenience.

My Solution:

Let $\angle BEP =E_1,\angle PEH = E_2,\angle AEH = E_3,\angle FEA = E_4 $

I will draw $$AG\bot BC \text{ , }PD\bot BC \text{,}AF\bot AG,FD\cap AB={E},EH\text{ bisector }\angle PEA$$so I will have $$FD||AG\to\angle BED=\angle BAG\text{ (Corresponding pair)}$$ We can easily calculate: $$\angle BED\text{ in }\triangle BED,\measuredangle BED=180^o-\angle EDB-(\measuredangle EBP+\measuredangle PBD)=180^o-90^o(30^o+24^o)=36^o(1)$$ But we have: $ \angle BED=\angle BAG $(Proved above) $\Rightarrow \measuredangle BAG =36^o$ and $EH$ bisector $\angle PEA\to \angle PEH = \angle AEH$ but we also have $$\angle BEP = \angle FEA = 36^o(\text{opposite angles})\Rightarrow \angle BEP+\angle PEA = 180^o \text{and}\angle FEA + \angle AEP =180^o(\text{both are complementary angle})$$ $$\to36^o + \angle PEA=180^o \text{and }36^o+\angle AEP = 180^o$$ or $E_2+E_3=144^o \text{ we also have EH bisector }\angle PEA\to E_2=E_3=72^o$ .On the other hand $EP||AI \text{ because }FD||AG\to\angle PEI =\angle EIA(\text{Alternate interior})\to\angle AEH = \angle AIH = 72^o\to \triangle AEI \text{ is a Isosceles triangle}$

Draw $AJ\bot EI\to AJ \text{ is also bisector }\angle EAI\to \angle EAJ = \frac{1}{2}\angle EAI =\frac{1}{2}\angle BAG=18^o $ $$\Rightarrow EAP = 18^o$$

Answer 5

We may conveniently partition $\angle BAC$ as $\angle BAP=18^\circ+\alpha$ and $\angle CAP=30^\circ-\alpha$, where $-18^\circ<\alpha<30^\circ$. Comparing the triangles $BAP$ and $CAP$, we note that $AP$ is common and $|BP|=|CP|$ (since $\triangle BPC$ is isosceles). Hence, applying the sine rule in a similar way to each triangle yields $\sin30^\circ\sin(30^\circ-\alpha)=\sin54^\circ\sin(18^\circ+\alpha)$, which may be written $$\cos60^\circ\cos(60^\circ+\alpha)=\cos36^\circ\cos(72^\circ-\alpha).\qquad\qquad(1)$$ It is well known that $\cos36^\circ=\frac14(\surd5+1)$ and $\cos72^\circ=\frac14(\surd5-1)$. (A proof is appended.) Hence $\cos36^\circ\cos72^\circ=\frac14=\cos^260^\circ$, and therefore $$\alpha=0$$ is a solution to eqn $1$. Also, the LHS of eqn $1$ is decreasing while the RHS is increasing in the given range for $\alpha$. Hence the solution $\alpha=0$ is unique.

Appendix$\quad$ A property of the cosine is that $$\cos(3\times72^\circ)=-\cos36^\circ=\cos(2\times72^\circ).$$ From the identities $\cos2\theta=2\cos^2\theta-1$ and $\cos3\theta=4\cos^3\theta-3\cos\theta$, it follows that $x=\cos72^\circ$ is a solution of the cubic $4x^3-3x=2x^2-1$, or $$(x-1)(4x^2+2x-1)=0.$$ Since $0<\cos72^\circ<1$, the linear factor may be ignored, and the required value is the positive root of the quadratic: $\cos72^\circ=\frac14(\surd5-1)$. The value $\cos36^\circ=\frac14(\surd5+1)$ follows from the initially mentioned properties.

Answer 6

Construct a regular pentagon on $BC$. Since $\angle ABC=54^o$, then $BA$ bisects $\angle FBC=108^o$, and $BAK$ is the perpendicular bisector of $GH$. Similarly, since $\triangle BPC$ is isosceles, $GPJ$, crossing $BK$ at $L$, perpendicularly bisects $BC$, and $FLM$ perpendicularly bisects $CH$.

Thus if we join $PH$, $AG$, and $AH$, we have $\triangle PGH\cong\triangle ABC$, and $\triangle HAG\cong\triangle BPC$.

By symmetry then, $\triangle LAP$ is isosceles. And since exterior $\angle KLG=180^o-90^o-54^o=36^o$, then $\angle LAP=\angle APL=18^o$.