2

I have a problem here solving this without trigonometry. We have an acute triangle. Is given the following. 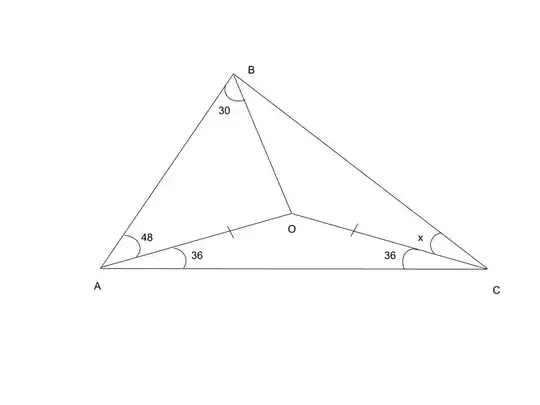enter image description here Find the $\angle$ BCO.

I tried different approaches. The continuation of CO intersects AB in point M, such that we get an isosceles triangle BMO. I have taken the mid-vertical of AB and found useful angles. I take P on AB such that the $\angle$ AOP = 48°. So I will get POS isosceles triangle with PO = OC and $\angle$ CPO = $\angle$ PCO = 6°. Let the intersection point of BO and CP be K. $\angle$ KOP = 18°. $\angle$ OKC = 24°. I have $\angle$ OCP, now I need to find $\angle$ BCK, to find x.

I tried other approaches also but still did not find the solution.

Zhenya Karapetyan
  • 99
  • 6
    What's the question? Write it in the body please. – user376343 May 20 '23 at 14:04
  • From the looks of it, it is possible to determine every angle, but no side lengths. Even using trigonometry as there are no given sides you will be unable to figure out the sides. – EzTheBoss 2 May 20 '23 at 14:22
  • I added the question in the body, we need to find the angle BCO. – Zhenya Karapetyan May 20 '23 at 16:19
  • 1
    The answer is $x = 18^\circ$, but I obtained it using trigonometry. But trig is just an application of geometry, so you could back out that trig solution to a strictly geometric solution. – Paul Sinclair May 21 '23 at 13:49
  • @PaulSinclair I tried to reverse engineer a solution from that too. It's indeed very easily found by using the law of sines for example... but working a purely geometrical argument from that is not so easy! I've been at it for a few days and I can't find a way to untangle all of the intermediate steps required. Any suggestions? :) On a side note, I really don't know why it was downvoted! I think it's completely legitimate & interesting to see how to do that problem without trigonometry. – Amit May 30 '23 at 13:36
  • 1
    @Amit - I don't know why it was downvoted either. The two close votes claim it is missing details, but likely these predate the current edit. The original question didn't indicate what the problem was asking to be found. I do not recall if the downvote occurred before I read it or not. If it was also before the edits that made the question clear, then I think it was appropriate, but if after, I do not agree with it either. But unfortunately, there are some denizens of this forum who practice the childish custom of drive-by downvoting (where no explanation is available). – Paul Sinclair May 30 '23 at 15:19
  • @Amit - As for backing out the trig solution to a geometric construction, I admit it would not be at all pretty. Effectively it would start with adding a couple perpendiculars to this diagram, but then would have to use additional diagrams effectively to demonstrate certain properties of the sine function. – Paul Sinclair May 30 '23 at 15:42
  • @PaulSinclair I have a possibly new direction involving the areas of various triangles, because I realized as I wrote the previous comment, areas proportions are the source of the law of sines. Either way I agree it may not look pretty :) – Amit May 30 '23 at 15:47
  • @Amit - using area proportions to prove the law of sines? That seems more convoluted than just calculating the height of the perpendicular to the third vertex twice and comparing the results. But it comes out to the same thing either way. – Paul Sinclair May 30 '23 at 16:05
  • @PaulSinclair no we're not supposed to prove it because we're supposed to be ignorant of the definition of the sine! :) but yeah, I get what you mean – Amit May 30 '23 at 16:15
  • First of all, thanks for your interest. This problem is eating my brain for 2 weeks now. I know that the answer is 24°. Maybe it can help us. I try to construct isosceles triangles to find angles. This is hard problem with simple rules. I would also like to know why is this question downvoted, because I have edited it properly:) – Zhenya Karapetyan May 31 '23 at 14:35
  • The answer is $18^{\circ}$ as @PaulSinclair noted. I verified it :) Perhaps you can edit your question to include the method you solved it with trig... – Amit May 31 '23 at 14:41
  • @PaulSinclair I tried using plain euclidean geometry, by not directly translating trigonometric values into lenght ratios. The graph is not too messy, I hope. – dfnu Jun 02 '23 at 10:31

2 Answers2

4

enter image description here

Construct the equilater triangle $\triangle BOD$ as shown above and produce $OC$ to $E \in BD$. Take $F\in CE$ in such a way that $AF\cong AO$.

  1. $AB$ perpendicularly bisects $OD$, hence $\measuredangle AOD = 42^\circ$, and $\triangle AOD$ is isosceles.
  2. Then also $\triangle DAF$ is isosceles, since $AF \cong AO \cong AD$.
  3. Angle chasing yields $\measuredangle AFC = \measuredangle FAC = 72^\circ$, so that $\triangle AFC$ is isosceles, too.
  4. We get $\measuredangle FAD = 60^\circ$, so by 2. $\triangle DAF$ is in fact equilateral.
  5. The quadrilateral $ACFD$ is thus a kite, whose diagonal $DC$ bisects its internal angles. Therefore, using 3., $\measuredangle OCD = 18^\circ$.
  6. Finally, since by angle chasing $\measuredangle EOD = 30^\circ$, $CE$ perpendicularly bisects $DB$; by 5., $$\measuredangle OCD = \boxed{\measuredangle OCB = 18^\circ}.$$
dfnu
  • 7,528
  • Why is $\triangle DAF$ isosceles? – Paul Sinclair Jun 02 '23 at 11:35
  • 1
    @PaulSinclair $AF \cong AO$ by construction, and $AO \cong AD$, by 1. – dfnu Jun 02 '23 at 11:39
  • 2
    Impressive, opened another horizon of mind!) – Zhenya Karapetyan Jun 02 '23 at 13:24
  • It's a really elegant solution, I was of late trying an approach that exploits the fact that $36^{\circ}$ happens to be $2\pi / 10$ so I tried to see if by drawing a diagram with such $10$ rotated copies of the triangle any new insight can come to mind. I guess I'll stop now :) But as an aside, this solution does make me wonder, whether this same construction you used, is the same that was used in constructing the problem :) – Amit Jun 02 '23 at 14:17
  • 1
    @Amit thanks for appreciating. You can also try with regular pentagons. See e.g. the similar problem https://math.stackexchange.com/questions/4705518/p-is-a-point-in-triangle-abc-with-angle-pbc-angle-pcb-24-circ-angl/4706568#4706568 – dfnu Jun 02 '23 at 15:18
3

Not the answer requested by the OP, but I thought it would be helpful to share the trigonometric solution:

First, let $a = AO = CO, b = BO$ and $y = \angle OBC$.

  • Adding the angles of $\triangle ABC$ yields $36^\circ + 36^\circ +48^\circ + 30^\circ + x + y = 180^\circ$, hence $y = 30^\circ-x$
  • Applying the law of sines to $\triangle AOB$ yields $\frac{\sin 30^\circ}{\sin 48^\circ} = \frac ab$.
  • Applying the law of sines to $\triangle BOC$ yields $\frac{\sin (30^\circ - x)}{\sin x} = \frac ab$.

Combining these gives $$\frac{\sin 30^\circ}{\sin 48^\circ} = \frac{\sin (30^\circ - x)}{\sin x}$$ Now $\sin (30^\circ - x) = \sin 30^\circ\cos x - \cos 30^\circ\sin x$ So $$\frac{\sin 30^\circ}{\sin 48^\circ} = \sin 30^\circ\cot x - \cos 30^\circ$$ $$\cot x = \frac 1{\sin 48^\circ} + \cot 30^\circ$$ which yields $x = 18^\circ$.

Paul Sinclair
  • 43,643