From what I'm guessing a keyhole contour is one that looks like this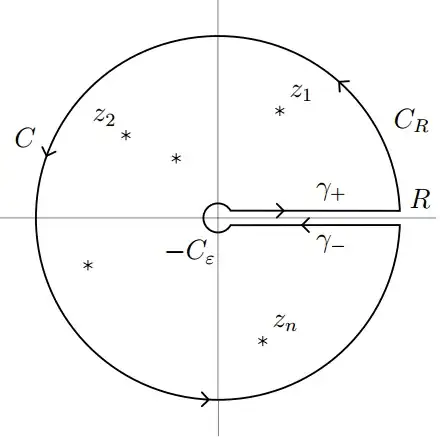
and because it can be shown that the contribution from $C_R$ and $C_\epsilon$ vanishes as $R\to \infty$, a Hankel contour looks like this.
If so, when I'm normally using a keyhole contour to solve improper integrals with bounds at infinity can I start it with something like this? $$\int_{\mathscr{H}}\frac{\ln z}{z^a(1+z)}\ dz=\int_{0}^{+\infty}\frac{\ln x}{x^a(1+x)}\ dx-\int_{0}^{+\infty}\frac{\ln x +2\pi i}{x^ae^{2\pi ia}(1+x)}\ dx$$ Where $\mathscr{H}$ is a Hankel contour surrounding $[0,\infty)$ in the clockwise sense.