Bessel function integral representation using Hankel's contour

Question

This question appears in a set of old qualifying exams I am using to practice.

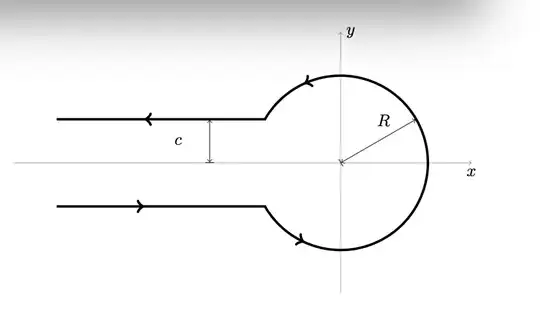
The Hankel path $H(c,R)$ is an infinite path that starts at a point at infinity $-\infty - ic$ to a point on a circle of $C_R$ radius $R$ ($0<c<R$) centered at the origin along the line $y=-c$, continuing along the an arc on $C_R$ to a point on the line $y=c$, and then to the point at infinity $\infty+ic$ along the line $y=c$.

The problem asks us to show that the Bessel function $J_\nu$ of order $\nu\in\mathbb{C}$ can be expressed as $$ J_\nu(z)=\frac{1}{2\pi i}\oint_{H(c,R)}\lambda^{-\nu-1}e^{\frac12 z\left(\lambda-\frac1\lambda\right)}\ d\lambda,\qquad \mathfrak{R}(z)>0$$

In the first part of the problem, we prove that the Gamma function satisfies $$ \Gamma(z)=\frac{1}{2 i\sin(\pi z)}\oint_{H(c,R)}\lambda^{z-1} e^\lambda\ d\lambda, \qquad z\in\mathbb{C}\setminus\mathbb{Z}.$$

Using this in combination with Euler's reflection formula $\Gamma(z)\Gamma(1-z)=\frac{\pi}{\sin \pi z}$ gives $$\frac{1}{\Gamma(z)}=\frac{1}{2\pi i}\oint_{H(c,R)}\lambda^{-z}e^\lambda \ d\lambda \qquad z\in\mathbb{C}.$$ Using Cauchy's integration theorem, we also have that the formulas above are independent of $c$ and $R$, i.e. we can deform $H(c,R)$ to any other Hankel path $H(c',R')$.

This allows us to rewrite $J_\nu$ as $$J_\nu(z)=\sum^\infty_{n=0}\frac{(-1)^n}{n!\Gamma(n+\nu+1)}\Big(\frac{z}{2}\Big)^{\nu+2n}= \frac{1}{2\pi i}\sum^\infty_{n=0}\frac{(-1)^n}{n!}\Big(\frac{z}{2}\Big)^{2n+\nu}\oint_{H(c,R)}\lambda^{-\nu-n-1}e^\lambda \ d\lambda.$$ By analytic continuation, it suffices to assume $z>0$. A change of variables $\lambda=\frac12 zw$ deforms $H(c,R)$ to $H(2z^{-1}c, 2z^{-1}R)$. This change of variables, provided that order of summation and integration can be inverted, gives $$J_\nu(z)= \frac{1}{2\pi i}\oint_{H(2z^{-1}c,2z^{-1}R)}\sum^\infty_{n=0}\frac{(-1)^n}{n!} \Big( \frac{zw^{-1}}{2}\Big)^n w^{-\nu-1}e^{\frac12 zw} \ dw.$$ The desired formula follows easily from this (Cauchy integration type arguments allow us to deform the path $H(2z^{-1}c,2z^{-1}R)$ back to $H(c,R)$).

Problem: I am having trouble justifying the change in the order of summation and integration. I am trying to use dominated convergence type of arguments but I am not getting very far. Any hints are appreciated. Thanks!

Answer 1

Assume that $z>0$ and choose the principal branch of $\operatorname{Log}$ which is defined on $P:=\mathbb{C}\setminus\{x+iy: y=0,x\leq 0\}$. Observe that the path of any Hankel loop $H(c',R')$ is contained in the principal domain $P$.

Define the function $$ G(w)=\sum^\infty_{n=0}\frac{(-1)^n}{n!}\frac{z^n w^{-n}}{2^n}w^{-\nu-1}e^{\frac{1}{2}zw} $$

Suppose $\nu=a+ib$. Then for any $w\in P$, $$|w^{-\nu-1}e^{\frac12zw}|=e^{\frac12z\mathfrak{R}(u)}e^{(-a-1)\log|w|+b\operatorname{arg}(w)}\leq e^{\frac12z\mathfrak{R}(u)}|w|^{-a-1}e^{|b|\pi} $$ Hence, $$|G(w)|\leq e^{|b|\pi}e^{\frac12z|w|^{-1}}|w|^{-a-1}e^{\frac12z\mathfrak{R}(w)}$$

integration over $H(c',R')$ yields \begin{align} \int_{H(c',R')}|G(w)||dw|&\leq 2e^{|b|\pi}\int^\infty_{a(c',R')}e^{\frac12z|t^2+(c')^2|^{-1/2}}|t^2+(c')^2|^{-\frac{a+1}{2}}e^{-\frac12zt}\,dt\\ &\qquad\qquad +\quad e^{|b|\pi}(R')^{-a}e^{\frac12zR^{-1}}\int^{\theta(c',R')}_{-\theta(c',R')}e^{\frac12zR'\cos s}\,ds<\infty \end{align} where $a(c',R')=\sqrt{(R')^2-(c')^2}>0$ and $\theta(c',R')=\operatorname{arg}(-a(c',R')+ic')$.

The conclusion then follows by dominates convergence.

---

Edit: Since $f(w)=w^{-\nu-1}e^{\frac12z(w-w^{-1})}$ is analytic on $\mathbb{C}\setminus(-\infty,0]\times\{0\}$, the integral representation of $J_\nu$ on $(0,\infty)\times\mathbb{R}$ is independent of the pair $c$, $R$ in $H(c,R)$. Although not part of the problem in the OP, it is interesting to notice that for $R=1$ and letting $c\rightarrow0$ one gets \begin{align} 2\pi iJ_\nu(z)&=\int^\infty_{a(c,1)}|t^2+c^2|^{-\frac{\nu+1}{2}} e^{-b\operatorname{arg}(-t-ic)} e^{-i(a+1)\operatorname{arg}(-t-ic)} e^{-\frac12z(t+ic-\frac{1}{t+ic})}\,dt\\ &\qquad - \int^\infty_{a(c,1)}|t^2+c^2|^{-\frac{\nu+1}{2}} e^{-b\operatorname{arg}(-t+ic)} e^{-i(a+1)\operatorname{arg}(-t+ic)} e^{-\frac12z(t-ic-\frac{1}{t-ic})}\,dt\\ &\qquad +i \int^{\theta(c,1)}_{-\theta(c,1)}e^{-i\nu\theta}e^{iz\sin\theta}\,d\theta\\ &\xrightarrow{c\rightarrow0} \int^\infty_1 t^{-(\nu+1)}e^{i\pi(\nu+1)}e^{-\frac12z(t-t^{-1})}\,dt - \int^\infty_1 t^{-(\nu+1)}e^{-i\pi(\nu+1)}e^{-\frac12z(t-t^{-1})}\,dt\\ &\qquad + i\int^\pi_{-\pi}e^{-i (\nu\theta-z\sin\theta)}\,d\theta\\ &=2i\int^\infty_1t^{-(\nu+1)}\sin(\pi(\nu+1))e^{-\frac12z(t-t^{-1})}\,dt+2i\int^\pi_0\cos\big(\nu\theta-z\sin\theta) \big)\,d\theta\\ &\stackrel{t=e^s}{=}-2i\sin(\nu\pi)\int^\infty_0 e^{-s\nu}e^{-z\sinh(s)}\,ds +2i\int^\pi_0\cos\big(\nu\theta-z\sin\theta) \big)\,d\theta \end{align} Putting things together, we obtain the well known formula $$ J_\nu(z)=\frac1\pi\int^\pi_0\cos\big(\nu\theta-z\sin\theta) \big)\,d\theta-\frac{\sin(\nu\pi)}{\pi}\int^\infty_0 e^{-s\nu-z\sinh(s)}\,ds,\qquad \mathfrak{R}(z)>0 $$

The justification can also be obtained by dominated convergence. I leave the OP to find a dominating function.