7

In radians the derivative of sine is the cosine. But why isn't this the same in degrees? According to this I'd first have to convert it to radians before this works. But when you look at the graph of sine whether the x is in degrees or radians, the graph stays the same... I don't understand.

user1534664
  • 1,272

3 Answers3

10

Here's a graph of $y = \sin x$.

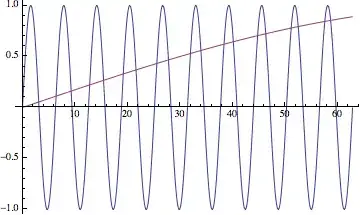
$y = \sin(x)$

The red line is $\sin x$ if $x$ is interpreted as an angle in degrees, and the blue line is $\sin x$ if $x$ is interpreted as an angle in radians.  See the difference?

Here's a zoomed-in version

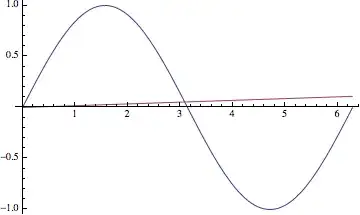
zoomed in version

What is $\sin(1.57\text{ rad}),$ and what is $\sin(1.57˚)?$

Intuitively, you can think of $\sin(x˚)$ as a "stretched out" version of the original graph. As a result, the slope of the tangent flattens, changing the derivative.

Ben Grossmann
  • 225,327
  • Thanks, I see the difference, but my question is actually, why are they different? – user1534664 Aug 13 '13 at 01:55
  • Well, let me ask you this: if $\frac{\pi}{2}\approx 1.57$, then what is $\sin(1.57)$ (1.57 in radians), and what is $\sin(1.57˚)$? – Ben Grossmann Aug 13 '13 at 01:57
  • 4
    @user1534664: the best way to think about sine, in the long term, is as a function from numbers to numbers. That function can be interpreted as taking an angle in radians and spitting out a ratio that relates to that angle. If you have an angle measured in degrees, you need to convert it to radians before you feed it to the sine function. $\sin(n^\circ)$ means $\sin\left(\frac\pi{180}n\right)$. Even better, you should always think of the $\phantom)^\circ$ symbol as meaning "times $\frac\pi{180}$". – dfeuer Aug 13 '13 at 01:59
  • sin(1.57degrees) = 0.0273.... and in radians its 0.0273 let me think about this lol – user1534664 Aug 13 '13 at 02:03
  • 1
    A good resource for teachers is The $\tau$ Manifesto (which also has cool art), but it's probably not the best for students. – dfeuer Aug 13 '13 at 02:03
  • 1
    @dfeuer so basically I should just accept that the sine function only accepts radians as its domain? and if I want the sin of a degree I need to convert it first? – user1534664 Aug 13 '13 at 02:06
  • 3
    I think the place to start is to accept that unless you specify otherwise, sin accepts radians as its domain. Radians, as it ends up, has a much more "natural" definition, to the point that can be thought of as not really being a unit, unlike degrees. So yes. The mathematical sine takes only radians. No degrees allowed, unless you change them into radians first. – Ben Grossmann Aug 13 '13 at 02:09
  • I miscalculated the sin of 1.57 in radians. It actually equals to 1, but in degrees its 0.0273. So that proofs they are different, just like the graphs. I think I'm just going to take your and dfeuers advice. I'll accept it as it is. Thanks! – user1534664 Aug 13 '13 at 02:25
  • 1
    @user1534664: to put one last spin on it, "degrees" is of the general nature as "dozen", "score", and "moles". You wouldn't expect the smell of three fish to equal the smell of three dozen fish, so you shouldn't expect the sine of three to equal the sine of three degrees. – dfeuer Aug 13 '13 at 02:54
  • @dfeuer When I say sin(90) on my calculator, and I have it on degrees mode and not radians, does the calculator automatically convert the 90 into radians? If not, I am confused. Thanks for your help, btw! – user1534664 Aug 13 '13 at 19:39
  • @user1534664, yes, "degree mode" on a calculator basically swaps out the trig functions with modified ones. It makes the sin and cos buttons calculate the $S$ and $C$ functions of Jean-Sébastien's answer, and does something similar with tan. It replaces $\sin^{-1}$ with the function $S^{-1}(x)=\frac{180}\pi sin^{-1}(x)$, etc. It's a convenience feature for people who need to deal with degrees a lot. – dfeuer Aug 13 '13 at 21:51
  • 1
    @dfeuer makes sense dude! So does this mean RAD is the default mode in mathematics? If I dont specify the ° sign it means its in radians? (not talking about the calculator here, I mean as when I write it down in a formula) – user1534664 Aug 13 '13 at 22:42
  • 1
    @user1534664, yes indeed. What makes radians so natural in geometry is this: if you draw a circular arc sweeping out some angle, then the radian measure of the angle is the length of the arc divided by its radius. $2\pi$ radians are a full turn because the circumference of a circle of radius $r$ is $2\pi r$. Analytically, it turns out that the sine function can be defined as $\sin x = x-{x^3\over3!}+{x^5\over5!}-{x^7\over7!}+\cdots$, which works only if $x$ is in radians. – dfeuer Aug 13 '13 at 23:07
3

I'm gonna assume that both system of measure exist, and that we all know that $$ \frac{\text{measure in degree}}{360}=\frac{\text{measure in rad}}{2\pi}. $$ I will also take for granted the classic derivative formulas for $\sin(x),\cos(x)\ldots$

It is often useful to think in terms of a new function to see this. There is no particular reason as to why they are not the same except that because that is the way the maths work. Nothing better to understand why something isn't true than to show it is not.

Let's define the degree sine function and call it $S(x)$ and the degree cosine function and call it $C(X)$. These are the functions that take $x$ degrees and return the value of $\sin(x°),\cos(x°)$. $\,S(x)$ corresponds to the red line in Omnomnomnom's answer. Now let us compute the derivative of $S(x)$, based on what we know. $$ \begin{align} \frac{d}{dx}S(x)&=\lim_{h\to 0}\frac{S(x+h)-S(x)}{h}&\\ & = \lim_{h\to 0} \frac{\sin(\frac{2\pi}{360}(x+h))-\sin(\frac{2\pi}{360}x)}{h} &\text{from measure to measure relation}\\ &=\frac{\pi}{180}\cos{\frac{\pi}{180}}=\frac{\pi}{180}C(x).& \text{from classic derivative formula} \end{align} $$ In a similar way, we'd find $C^{'}(x)=-\frac{\pi}{180}S(x)$.

Some not directly related but similar reading about radians vs degrees can be found here and also here.

Jean-Sébastien
  • 4,623
  • 1
  • 17
  • 39
  • 3
    Why muck with those limits if you're just going to use the chain rule and known derivatives in the end? – dfeuer Aug 13 '13 at 04:55
  • 1
    @dfeuer This was tagged as pre-calculus, I had no idea what was known to the op. He knew derivative, so I went with the basic definition. – Jean-Sébastien Aug 13 '13 at 05:03
-4

this is because of the contraction of the functions as the domain changes. in degrees 0 to90 corresponds to 0 to 3.14 radians hence suitably as the general derivative is made with radians as domains we have convert other units into the general.

Suraj M S
  • 1,891