Stewart's theorem states that in the triangle shown below,
$$ b^2 m + c^2 n = a (d^2 + mn). $$
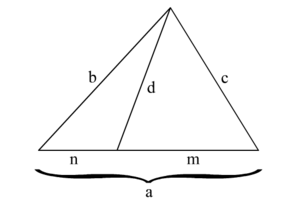
Is there any good way to prove this without using any trigonometry? Every proof I can find uses the Law of Cosines.
Stewart's theorem states that in the triangle shown below,
$$ b^2 m + c^2 n = a (d^2 + mn). $$

Is there any good way to prove this without using any trigonometry? Every proof I can find uses the Law of Cosines.
You can do it using the Pythagorean theorem. I'll treat the case in which $\angle (a,b)$ and $\angle(a,c)$ are both acute and $m \gt n$ as in your figure.
Draw the height $h$ of the triangle $abc$ and denote the resulting middle segment on $a$ by $x$. Using the Pythagorean theorem one sees
$$\begin{align*} b^2 &= h^2 + (n+x)^2 \\ c^2 &= h^2 + (m-x)^2 \\ d^2 &= h^2 + x^2 \end{align*}$$
Therefore $$\begin{align*} b^2 m &= h^2m + n^2m + 2mnx+x^2m \\ c^2 n &= h^2n + m^2n - 2mnx + x^2n \\ b^2 m + c^2n &= (n+m)(h^2 + mn + x^2) = a(d^2 + mn) \end{align*}$$ as we wanted.
If $\angle(a,c)$ is obtuse, the same idea works: Write $$b^2 = (m+n+x)^2 + h^2, \qquad c^2 = x^2 + h^2, \qquad d^2 = (m+x)^2 + h^2$$ and calculate similarly.
Symmetry and the consideration of some degenerate cases easily lead to a complete proof of Stewart's theorem from what I've written here.
It would be very nice to have a good pictorial proof that makes the identity similarly obvious as Pythagoras, but so far I couldn't come up with a nice figure that would achieve this.
Added: Matthew Stewart (1717–1785) published this theorem as Proposition II on page 2 in his 1746 book Some general theorems of considerable use in the higher parts of mathematics (arxive.org). Unfortunately, Google's scans don't seem to include the figures, but they are easy to reconstruct from the description in the text.
Update:(by @brainjam) I've taken the liberty of adding a partial scan of the figures from another Google scan -
One case of Stewart's Proposition II reads in the above notation:
$$b^2 + c^2 \frac{n}{m} = an + d^2 \frac{a}{m}$$
and it has the following nice corollary:
$$a^2 + b^2 + c^2 = 2d^2 + m^2 + n^2.$$
Here's the title page and the relevant passage (not using trigonometry either). Since Proposition I is used in the proof, I'm including the entire beginning of the text:
First of all, see the Wikipedia article Stewart's Theorem. I personally prefer the symmetric formulation of the theorem, because it is easy to remember without any mnemonic trickery:
Let $A$, $B$, $C$ be points on a directed line $l$ in the Euclidean plane, and $P$ be a point anywhere in the plane. Then $$ PA^2\cdot BC + PB^2\cdot CA + PC^2\cdot AB + BC\cdot CA\cdot AB = 0~, $$ where the length of a line segment $XY$ on the line $l$ is positive if the segment has the same direction as the line, and is negative if it has the opposite direction.
Proof. The proof is by straightforward calculation. Choose a Cartesian coordinate system with the directed line $l$ as the first axis, and let the points involved have the coordinates $A=(a,0)$, $B=(b,0)$, $C=(c,0)$, $P=(x,y)$. Stewart's identity is essentially just the polynomial identity $$ (1) \quad (x-a)^2(c-b) + (x-b)^2(a-c) + (x-c)^2(b-a) + (c-b)(a-c)(b-a) = 0~, $$ which is easily verified. (Go and really do the calculation: it's fun to observe everything cancel out.) Now add to the above identity the obvious identity $$ y^2(c-b) + y^2(a-c) + y^2(b-a) = 0~, $$ and you have the full-blown Stewart's theorem. Done.
Note that the theorem is true also in partly degenerate situations, where some of the points $A$, $B$, $C$ coincide, or the point $P$ is on the line $l$. A geometric reasoning has to discuss these degenerate cases separately, while the computational proof smoothly subsumes them in the general case.
Remark. The identity $(1)$ is a generic polynomial identity, which means that it is an identity in the ring $\mathbb{Z}[a,b,c,x]$ of polynomials in (formal) variables $a$, $b$, $c$, $x$ with integer coefficients, and therefore instantiates to an identity when the variables are replaced by elements of an arbitrary commutative ring. This observation tells us that Stewart's theorem is valid in the 'Euclidean plane geometry' over any commutative ring, in particular over any field.
Geometric equivalents of the Law of Cosines are already present in Book II of Euclid, in Propositions $12$ and $13$ (the first is the obtuse angle case, the second is the acute angle case).
Here are links to Proposition $12$, Book II, and to Proposition $13$.
There is absolutely no trigonometry in Euclid's proofs.
These geometric equivalents of the Law of Cosines can be used in a mechanical way as "drop in" replacements for the Law of Cosines in "standard" proofs of Stewart's Theorem. What in trigonometric approaches we think of as $2ab\cos\theta$ is, in Euclid, the area of a rectangle that is added to or subtracted from the combined area of two squares.
If you can get your hands on M. S. R. Anjaneyulu, Elements of Modern Pure Geometry, Asia Publishing House, New York 1964 (MR0172146 (30 #2372)), it may have what you want. The review, by Coxeter, starts, "This is a nicely written text-book. The work begins with directed line segments, Stewart's theorem, and a metrical definition for the harmonic relation...." and the review never mentions trigonometry.