Similarity of Triangle problem

Question

Given: AD & PS are medians in ΔABC and ΔPQR respectively,
$$\frac{AB}{PQ}=\frac{AD}{PS}=\frac{AC}{PR}$$

To Prove: ΔABC ~ ΔPQR

Figure:

Triangles Image

Problem: In ΔABD & ΔPQS or in ΔADC & ΔPSR or in ΔABC & ΔPQR, I have only found that only two sides are proportional but can't figure-out third thing to prove similarity.

Plz help me.

I would use the cosine law to prove that one of the angles at $A$ equals one of the angles at $P$ — Ross Millikan, Jun 29 '11 at 04:34
@Ross: Its a 10th standard question and students don't know trignometry, any other way to prove... — Javed Akram, Jun 29 '11 at 04:40
Since D is the midpoint of BC and S the midpoint of QR, you know that BD = DC, QS = SR. So BD/QS = DC/SR ... — amWhy, Jun 29 '11 at 04:50
You have to use (somehow) the fact that BDC and QSR are straight lines ie that the angles at D (and angles at S) are supplementary. It is possible (easy) to create a configuration where the ratios are equal and QS = QR but QSR is not straight - so straightness is essential. — Mark Bennet, Jun 29 '11 at 05:01

score 7 · Accepted Answer · edited Jun 29 '11 at 13:41

7

Create a point A' in the direction of AD, such that DA'=AD. Then there is a parallelogram ABA'C. So is parallelogram PQP'R.

Image made with Geogebra

And AD/PS=AA'/PP',
So, AB/PQ=AA'/PP'=AC/PR.
=>ΔABA' ~ ΔPQP'
=>∠BAD=∠QPS
So is ∠CAD=∠RPS
Then ∠BAC=∠QPR
=>ΔABC ~ ΔPQR
(Q.E.D.)

edited Jun 29 '11 at 13:41

ShreevatsaR

41,374

answered Jun 29 '11 at 06:07

puresky

419

Nice clean solution. – André Nicolas Jun 29 '11 at 13:19
thanx @puresky, very very fine solution. – Javed Akram Jun 29 '11 at 13:38
1

I've added an image (created with Geogebra; please feel free to remove or replace with better image or whatever. – ShreevatsaR Jun 29 '11 at 13:42
1

Thanx @ShreevatsaR. It's nice of you for helping to make it clear. – puresky Jun 30 '11 at 05:27

score 4 · Answer 2 · edited Apr 13 '17 at 12:21

4

We can use a special case of Stewart's Theorem, which has a non-trigonometric proof recently discussed on Stack Exchange.

I will therefore write out a sketch of a trigonometric proof of the result, in the knowledge that the trigonometry can be eliminated.

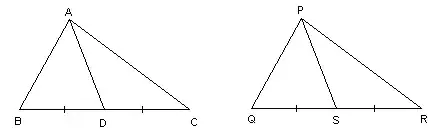
To make our lives easier, so we don't have to work with ratios, scale one of the triangles to make $AB=PQ$. The other sides that were in the same ratio then also become equal. So now we want to prove congruence. Then we can scale back to get similarity.

Look at the left triangle, and let $AB=c$, $AC=B$. Let $AD=d$, and let $BD=DC=u$.

Consider $\triangle ADB$, and let $\theta$ be the angle at $D$.

By the Cosine Law, $$c^2=d^2+u^2-2du \cos(\theta).$$

Now in $\triangle ADC$, the angle at $D$ has cosine the negative of $\cos(\theta)$, so again by the Cosine Law, $$b^2=d^2+u^2+2du\cos(\theta).$$

Add, sneakily letting $\theta$ drop out of the picture. We get $$c^2+b^2=2(d^2+u^2).$$

Comment: To get rid of the trigonometry, we can drop a perpendicular to $BC$ from $A$. Then two applications of the Pythagorean Theorem give us the fact that $c^2+b^2=2(d^2+u^2)$, which will turn out to be what we need. (The details of the calculation are done one of the Stewart's Theorem answers referred to earlier.)

In the other triangle, let $v=QS=SR$. Remember that the other sides are equal to the corresponding sides of the first triangle, because of the scaling. Thus $$c^2+b^2=2(d^2+v^2).$$

It follows that $u=v$, and we are finished.

edited Apr 13 '17 at 12:21

Community

1

answered Jun 29 '11 at 05:00

André Nicolas

507,029

There is a name for what you got: Appolonius Theorem – Aryabhata Jun 29 '11 at 05:14
@Aryabhata: Thanks for the name. I will stick with the name of the generalization, because of the happy accident that it was recently discussed on this site. – André Nicolas Jun 29 '11 at 05:21
2

Am I right that there is a much simpler proof based on amWhy's comment? Wouldn't the triangles be similar even if we weren't told $AD/PS$ is equal to those other ratios? – Gerry Myerson Jun 29 '11 at 06:03
@Gerry Myerson: There are inequality-based proofs that use less machinery. If you want to get rid of the middle term, you certainly need to add something. – André Nicolas Jun 29 '11 at 06:58
@user6312, thanks, but I don't see where a proof based on amWhy's comment uses anything about $AD/PS$. What am I missing? Is there a counterexample? – Gerry Myerson Jun 29 '11 at 13:09
I think this is a much more complicated proof than necessary. Stewart's Theorem shouldn't be needed. See puresky's proof. – ShreevatsaR Jun 29 '11 at 13:35
@Gerry Myerson: The fact that $AB/PQ=AC/PR$ by itself says nothing, almost everything is a counterexample. Make $AB=PQ$, $AC=PR$, pick different angles at $A$ and $P$, draw the medians. The picture is a bit misleading, seems to indicate $BD=QS$, but text does not say so. Even with equality, counterexample is immediate without the information about $AD/PS$. – André Nicolas Jun 29 '11 at 13:39
@ShreevatsaR: I have seen it, had left a comment to puresky praising the solution. – André Nicolas Jun 29 '11 at 13:59

Similarity of Triangle problem

2 Answers2