Proof of Stewart's Theorem using elementary geometry

Question

I was reading Stewart's Theorem which states that

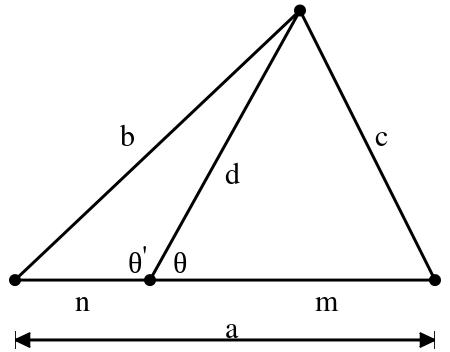
Given a triangle with side lengths $a$, $b$, $c$ and a cevian of length $d$ which divides $a$ into two segments $m$ and $n$ as shown in the figure

we must have $$b^2m+c^2n=a(d^2+mn)$$ which is often remembered using the funny mnemonic, "A man and his dad put a bomb in the sink" which gives $$man+dad=bmb+cnc$$

Now, this can be proved quite easily using The Law of Cosines on $\theta$ and $\theta^\prime$ as marked in the figure. You can find the proof here.

But, I was thinking if there is a more elementary geometric argument (without using trignometry and without using a lot of algebraic manipulation) to see this clearly in front of our eyes. I tried giving an attempt, but it seems extremely difficult using only elementary geometry since there is no trivial symmetry immediately observable in this diagram. Also, the terms involved in the formula, i.e., $b^2m$, $c^2n$, $ad^2$ and $amn$, are all of dimension $[L^3]$- so, it seems difficult to even draw areas on sides and geometrically manipulate them.

Any elegant geometric insight or an intuitive idea would be appreciated.

Note: as pointed out in the comments, and as you can see here as well, the Cosine Law can be very well proved using elementary geometry. While that is of course an answer, we all agree that it's cheating at some level. There's another answer as well, but this one's so much algebraic jargon, I would prefer trigonometry instead.

Also, Stewart's book, Some general theorems of considerable use in the higher parts of mathematics seems to contain a completely geometric argument. But the absense of diagrams in Google Scans combined with the length of this solution makes it very difficult to follow. I would also love to see a summarized version of this in more understandable way without loosing the geometric essence.

Answer 1

$\triangle ABC$ is our reference triangle. Draw the circle centered at $A$ with radius $c$. Extend segments as shown in the figure. Using the power of a point at points $D$ and $C$, we get two equations:

$$c^2-x^2=m\cdot (n+y) \;\; \text{and} \; \; c^2-b^2=(m+n)\cdot y$$

Solving simultaneously (eliminating $y$) yields Stewart's Theorem. $\;\blacksquare$

---

What is meant by elementary geometry is rather controversial (power of a point $=$ similarity).

Answer 2

Write $m:=a\mu$ and $n:=a\nu$. The highlighted similar triangles $\triangle A'DB$, $\triangle B''B'B$, $\triangle C''C'A$ in the figure (whose construction is detailed below) have corresponding sides in proportion, say, $\lambda:\mu$; we deduce $\triangle ABC\sim\triangle B''BA'$, so that $|A'B''|=b\lambda=|AC''|$, and we can write $|AA'|=|AC''|+|AB''|$.

Now, we simply apply the Intersecting Chords/Secants theorems thusly

$$ \begin{align} \color{green}{a\mu\cdot a\nu} = \overbrace{\color{green}{|AD|\,|A'D|}}^{\bigcirc ABC} &= |AD|\,(\,|AA'|-|AD|\,) \\[0.5em] &= |AD|\,(\,\color{blue}{|AC''|}+\color{red}{|AB''|}-|AD|\,) \\[0.5em] &=\overbrace{\color{blue}{|AC|\,|AC'|}}^{\bigcirc CC'C''}+\overbrace{\color{red}{|AB|\,|AB'|}}^{\bigcirc BB'B''} - |AD|^2 \\[0.5em] &=\color{blue}{b\cdot b\mu}+\color{red}{c\cdot c\nu} - d^2 \tag{$\star$} \end{align}$$

giving the equivalent of Stewart's Theorem. $\square$

---

The diagram is created by extending cevian $\overline{AD}$ to meet the circumcircle at $A'$. Then $B'$ and $C'$ divide $\overline{BA}$ and $\overline{AC}$ in the ratio $\mu:\nu$, and circumcircles $\bigcirc DBB'$ and $\bigcirc DCC'$ meet the cevian in points $B''$ and $C''$. A little angle-chasing establishes the similarity of the highlighted triangles.

Admittedly, that's quite a bit of setup —and perhaps there's an easier path to the key relation $|AA'|=|AB''|+|AC''|$— but I rather like how $(\star)$ falls right out.

Answer 3

I have found a proof through Ptolemy's theorem and the intersecting chords theorem, but it is rather messy, sketched in the following diagram (beware: I accidentally swapped $m$ and $n$)

Let us consider two spiral similarities bringing $ACD$ to $ABE$ and $ADB$ to $AFC$. Since we have supplementary angles at $D$, $ADBE$ and $AFCD$ are similar and cyclic. Their sides and diagonals are proportional to the sides and diagonals of the purple quadrilateral in the top right. The lengths of the diagonals are fixed by Ptolemy's theorem. Let us consider the intersection $K$ between $AD$ and the circumcircle of $ABC$: the quadrilateral $ABKC$ is similar to the quadrilateral with the orange diagonal, so $AK=\frac{c^2 m+b^2 n}{ad}$. On the other hand, by the intersecting chords theorem, $AK=d+\frac{mn}{d}$. This proves Stewart's theorem.

Answer 4

Comment:

This can be proved easily when triangle is right angled; suppose the foot of height is H, we have:

$$\triangle AHB\approx \triangle ACH$$

which results in:

$$ \frac bc=\frac c m\Rightarrow bm=c^\space\space\space\space\space\space\space(1)$$

$$\frac cd=\frac bn \Rightarrow cn=bd\space\space\space\space\space\space\space(2)$$

$$d^2=mn\space\space\space\space\space\space\space\space (3)$$

$bm=c^2\Rightarrow b^2m=(bc)d=2s\cdot c$

$cn=bd\Rightarrow c^2n=(bc)d=2s\cdot d$

$\Rightarrow bm^2+cn^2=2s(d+c)=d\cdot a (d+c)=a(d^2+c\cdot d)$

Multiplying (1) by (2) we obtain:

$bc(mn)=bc\cdot cd$

$\Rightarrow mn=cd$

Which gives:

$$b^2m+c^2n=a(d^2+mn)$$

This is true for all right angled triangles constructed when vertex A moves on a circle its diameter is BC.If we keep BC constant, the fact that this relation is correct for all types of triangles shows that any arbitrary transformation of a right angled triangle, keeping BC constant, to any arbitrary shape keeps the quantity the formula describe.