In mathcounts teacher told us to use the formula $ \sin2x=2 \sin x \cos x$. What's the math behind this formula that made it true? Can someone explain?
8 Answers
 $$\color{red}{\sin 2x}=\color{blue}{2\sin x}\cos x$$
$$\color{red}{\sin 2x}=\color{blue}{2\sin x}\cos x$$
- 53,234
- 13
- 164
- 223
-
5Wow this makes much more sense!! Thanks man! – Commander Shepard Aug 05 '13 at 14:48
-
2Sorry i don't get it... – David G Aug 05 '13 at 15:35
-
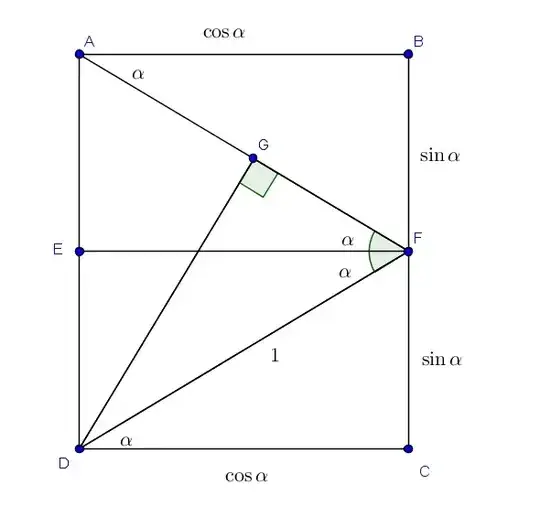
10@David There are two ways to calculate the red thing: 1) from the right triangle with hypotenuse $1$ (this gives $\sin 2x$) and 2) from the complementary right triangle with blue hypotenuse, equal to $2\sin x$. – Start wearing purple Aug 05 '13 at 15:37
-
6I can't believe I've never seen this before. Amazing! – Steven Stadnicki Aug 05 '13 at 21:19
-
1Cool diagram. Quite a simple and elegant geometric demonstration. – Pratyush Sarkar Aug 07 '13 at 23:32
-
1How about when $x\notin [0,\frac{\pi}{2}]$? – R R Dec 02 '13 at 23:59
$$\sin(2x)=\mathrm{Im}(e^{2ix})=\mathrm{Im}(e^{ix}e^{ix})=\mathrm{Im}((\cos x+i\sin x)(\cos x+i\sin x))=2\sin x\cos x$$
-
3$e^{i\phi} = cos \phi + i sin \phi?$ This is Euler's formula, the greatest formula in the whole math! You must always use it to prove trigonometric relationships and integral calculus as it gives simplest and most beatiful solutions and teaches you the imaginary unit! – Val Aug 05 '13 at 19:34
-
3And for a simple trig problem like this is is extravagant overkill. – marty cohen Aug 07 '13 at 23:13
-
2@martycohen Not really. It gets the result quickly without any need for geometric cleverness. – Potato Aug 08 '13 at 00:40
-
1+1: This method also gives all of the double-angle (and triple-angle, etc.) formulas. – Neil G Aug 14 '13 at 22:28
-
2If we think of usual definition of $\sin x, \cos x$ (i.e. as coordinates of a point revolving on a circle of unit radius), then it is impossible to derive the Euler's formula without the use of addition rules like $\sin(a + b) = \sin a \cos b + \cos a \sin b$. So it becomes circular reasoning. On the other hand if we use the infinite series for $\sin x, \cos x$ as their definition then this is not circular. But I still believe OP did not have infinite series definition in mind. – Paramanand Singh Nov 10 '13 at 11:42
Assuming that you already know the sum of angles formula, this is pretty easy to get:
$\sin(x + y) = \sin(x)\cos(y) + \cos(x)\sin(y)$, so
$\sin(2x) = \sin(x + x) = \sin(x)\cos(x) + \cos(x)\sin(x) = 2\sin(x)\cos(x)$.
Edit: If you don't want to take the sum of angles formula for sines as a given, this page on Wikipedia can explain it better than I can, especially since it has a diagram.
- 3,890
-
1
-
1@Blue those pictures are fantastic, thank you. These deserve more exposure. – littleO Aug 07 '13 at 23:28
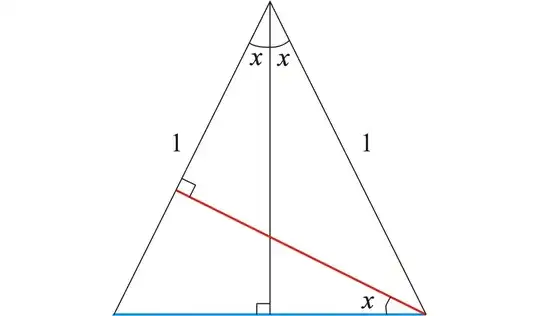
Geometrically, the area of an isosceles triangle with apex $2\alpha$ and leg length $1$ can be computed with one of the legs as base, then the height is $\sin 2\alpha$. So th earea is $\frac12\sin 2\alpha$.
Alternatively, the base has length $2\sin \alpha$ and the corresponding height is $\cos \alpha$, thus the area is $\frac12\cdot2\sin\alpha\cos\alpha$.
Equating both, you get $\sin2\alpha=2\sin\alpha\cos\alpha$.
- 374,180
A rotation matrix is clearly a linear transformation, so by rotating the elementary basis vectors, a two-dimensional rotation matrix for angle $x$ is \begin{align} \begin{bmatrix} \cos(x) & -\sin(x) \\ \sin(x) & \cos(x) \end{bmatrix}. \end{align}
Squaring this matrix is equivalent to applying the rotation twice, so \begin{align} \begin{bmatrix} \cos(2x) & -\sin(2x) \\ \sin(2x) & \cos(2x) \end{bmatrix} &= \begin{bmatrix} \cos^2(x) - \sin^2(x) & -2\sin(x)\cos(x) \\ 2\sin(x)\cos(x) & \cos^2(x) - \sin^2(x) \end{bmatrix}, \end{align} which implies that \begin{align} \cos(2x) &= \cos^2(x) - \sin^2(x) \\ \sin(2x) &= 2\sin(x)\cos(x). \end{align}
Using rotation matrices with different angles gives some of the double-angle (or triple-angle, etc.) identities.
- 2,479
All of those weird trigonometric identities make sense if you express them as exponentials.
$$\sin 2x = 2\sin x \cos x. $$
Using $e^{xi} = \cos x + i\sin x $ and expressing $\cos$ and $\sin$ through this...
\begin{align} &\frac{e^{2xi} - e^{-2xi}}{2i} = 2 \frac{e^{xi} - e^{-xi}}{2i} \frac{e^{xi} + e^{-xi}}{2},\\ &\frac{e^{2xi} - e^{-2xi}}{2i} = \frac{(e^{xi} - e^{-xi})(e^{xi} + e^{-xi})}{2i},\\ &\frac{e^{2xi} - e^{-2xi}}{2i} = \frac{e^{2xi} - e^{-2xi}}{2i}. \end{align}
Of course, the geometric interpetation makes more sense here.
- 53,234
- 13
- 164
- 223
- 131
Let's start with the power series definitions: $$\sin x=\sum_{n=0}^\infty (-1)^n \frac{x^{2n+1}}{(2n+1)!}=x-\frac{x^3}{3!}+\frac{x^5}{5!} -+ \dots, $$ $$\cos x=\sum_{n=0}^\infty (-1)^n \frac{x^{2n}}{(2n)!}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-+ \dots. $$ If you expand the product $$\sin x \cos x= \left( x-\frac{x^3}{3!}+\frac{x^5}{5!} -+ \dots \right) \left( 1-\frac{x^2}{2!}+\frac{x^4}{4!}-+ \dots \right), $$ and collect terms, you will find that only odd powers of $x$ appear, and the coefficient of $x^{2n+1}$ is $$(-1)^n \left(\frac{1}{(2n+1)!0!}+\frac{1}{(2n-1)! 2!}+ \dots +\frac{1}{1!(2n)!} \right).$$ You can prove (using induction for example) that the last expression equals $$(-1)^n \frac{2^{2n}}{(2n+1)!}=(-1)^n \frac{1}{2} \frac{2^{2n+1}}{(2n+1)!}.$$ Thus we have $$\sin x \cos x=\frac{1}{2} \sum_{n=0}^\infty (-1)^n \frac{(2x)^{2n+1}}{(2n+1)!}, $$ which is precisely $\frac{1}{2} \sin 2x$.
- 24,381