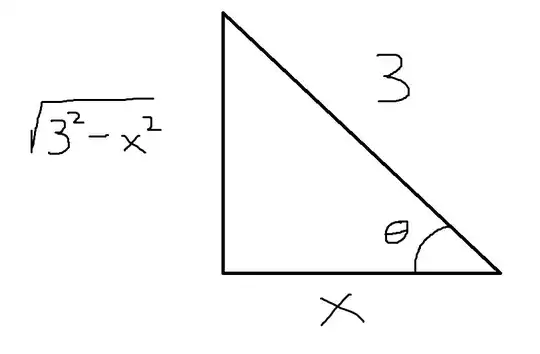4

I'm looking to simplify $$\sin(2\cos^{-1}{(x/3)})$$

I know it simplifies to $\frac{2x}{3}\sqrt{1-\frac{x^2}{9}}$, but I am unsure of the required steps.

Thanks for any help

user103828
  • 2,368
nuggetbram
  • 581
  • Are you sure of your expected answer of $6x/(x^2+9)$? If I plug in x = 1, I get approx $0.6285$ in the trig version, and $6/10 = 0.6000$ in the expected answer. – Brian J Apr 22 '15 at 14:15
  • Just realised I'd typed in the wrong solution! The correct one is now there – nuggetbram Apr 23 '15 at 06:55

3 Answers3

5

Use the double-angle formula, $$ \sin{2\theta} = 2\sin{\theta} \cos{\theta}. $$ What happens to the $\cos$ is clear. To deal with the sine, recall that $$ \cos^{2}{\theta}+\sin^2{\theta} = 1, $$ with which you can rewrite the sine, after you verify which sign of the square root. The answer you should find is $$ \frac{2x}{3}\sqrt{1-\frac{x^2}{9}}. $$

Chappers
  • 67,606
1

$$\sin (2\cos^{-1}y)=2y\sin(2\cos^{-1}y)=2y\sqrt{1-y^2}$$where in the first step I have used $\sin 2\theta =2\sin \theta \cos \theta$ and in the second step I have used $\sin^2\theta+\cos^2\theta=1$

Samrat Mukhopadhyay
  • 16,277
0

(If you don't remember that $\sin({2\theta})=2\sin\theta\cos\theta$, you can look here for helpful proofs.)

An alternative after converting the equation to $2\sin\theta\cos\theta$, where $\theta=\cos^{-1}(x/3)$, is to draw a triangle to solve for the missing pieces.

Assume the reference angle is $\theta$. Then draw $\cos^{-1}(x/3)$ where $x$ is the adjacent side, and $3$ is the hypotenuse. Using Pythagorean's Theorem, we see the opposite side is $\sqrt{3^2-x^2}$. Thus, $\sin\theta$, being opposite over hypotenuse, is $(\sqrt{3^2-x^2})/3$. The $\cos$ will cancel out with each other to get $x/3$.

From there, multiply the terms together: $2 * ((\sqrt{3^2-x^2})/3) * (x/3)$.

enter image description here

Community
  • 1
Brian J
  • 319