12

I want to write a program that calculates the number of zeros (It is not necessary to identify them, just the number of them) between 0 and x for the Riemann Zeta function, being x the imaginary part of z: 1/2 + ix

Is there an algorithm out there for doing what I need?

I modelled the Riemann-siegel function because I saw that I need it for doing what I want, but I don't know how to go on.

Sorry for my poor english :/

Perroloco
  • 223
  • 6
    The Riemann zeta is defined on the complex plane, so looking for the "number of zeros between $0$ and $x$" doesn't make a whole lot of sense. I think you have a lot of reading to do before you try this. – Gyu Eun Lee Jul 12 '13 at 22:57
  • 1
    I do not think there is a known algorithm for that, but I wish you good luck! – AD - Stop Putin - Jul 12 '13 at 23:01
  • 1
    The zeros of $\zeta(s)$ are the negative even integers and the nontrivial zeros that lie in the so-called critical strip $0<{\rm Re}(s)<1$ (it is conjectured that all the nontrivial zeros in fact lie on the critical line ${\rm Re}(s)=1/2$). There are algorithms that calculate the number of zeros in the strip with imaginary part less than $N$ (and there is current research in the asymptotics and statistics of this counting function in analytic number theory). It is also possible to verify computationally that known zeros have real part exactly (not just approximately) $0.5$. – anon Jul 12 '13 at 23:08
  • If you are really asking about the real interval $(0,x)$, then this suggests you're not at all familiar with complex analysis and the Riemann zeta function, which begs the question of why you want an algorithm for this purpose. As the content of my previous comment establishes, the answer is "for any $x>0$ there are precisely no zeros of $\zeta(s)$ at all in the interval $(0,x)$." Furthermore if one is unfamiliar with analytic continuation, it won't make sense how $\zeta(s)$ is even defined for $0\le s\le 1$, since the $p$-series doesn't converge there. – anon Jul 12 '13 at 23:12
  • thanks for the help. I changed the question...i hope it's more understandable now! – Perroloco Jul 13 '13 at 01:38

4 Answers4

9

You may appreciate the following '$\zeta$ zeros counting function' if $t$ is the imaginary part : $$f(t) = \frac{1}{\pi} \Im\left(\ln(\Gamma\left(\frac 14 + \frac{i\,t}2\right)\right) - \frac{t}{2\pi}\ln(\pi) + \frac{1}{\pi} \Im\left(\ln\left(\zeta\left(\frac 12 + i\,t\right)\right)\right) + 1$$ Explication : if we multiply this by $\pi$ we note that the first imaginary term combined to the next term returns the actual argument of $\zeta$ (this is the well known Riemann–Siegel theta function) that grows with high regularity while the imaginary term at the right gives the argument of $\zeta$ modulo $2\pi$ which will change sign for every multiple of $\pi$ (that is at every zero of $\zeta$ !).

More about the way this formula was obtained here.

Illustration using the pari/gp code at the end (zoom possible) :

zeros counting function

The first step is between $14.1$ and $14.2$, the second between $21$ and $21.1$ and so on so that we are really counting the zeros of $\zeta$...

The picture is not always so nice and, from time to time (starting after $t=415$ I think), there will be a non-propagating error of $\,\pm 2\,$ when $\,\displaystyle\frac 1{\pi}\rm{Arg}\;\zeta(1/2+it)\;$ crosses the upper bound $+1$ or lower bound $-1$ (so that this appears rather when two consecutive zeros are distant i.e. for large loops as displayed in the other answer).

This formula was in this MO thread with further references to Guinand's article : 'A summation formula in the theory of prime numbers'.

pari/gp code used for the picture :

f(t)=imag(lngamma(1/4+I*t/2))/Pi-t/(2*Pi)*log(Pi)+imag(log(zeta(1/2+I*t)))/Pi+1
Community
  • 1
Raymond Manzoni
  • 43,021
  • 5
  • 86
  • 140
  • Raymond, Does your Riemann zeta zero counting plot work also in the interval from t=278 to t=285 ? – Mats Granvik Nov 06 '15 at 14:30
  • What I mean is this: http://math.stackexchange.com/questions/1516149/is-this-plot-of-the-argument-of-the-riemann-zeta-function-around-zetazero127-c/1516167#1516167 – Mats Granvik Nov 06 '15 at 15:36
  • The zero counting formula as written is not perfect and I observe the same jump of $2$ than in your first link. As indicated by Henning Makholm in your recent thread (or in my answer here!) your software uses the principal value to compute the argument of $\zeta$ with the problem that it may shortly go out of $,(-\pi,\pi],$ like for \begin{align}\arg \zeta(1/2+282.45 i)&\approx -3.1326099\\arg \zeta(1/2+282.46 i)&\approx +3.1315472\end{align} (jump of $2\pi$). If you subtracted $2\pi$ to the values near $+\pi$ you would get instead – Raymond Manzoni Nov 06 '15 at 22:46
  • $$\arg \zeta(1/2+282.46 i)\approx -3.1516381$$ and the steps would appear perfect with the usual jump of $\pi$ for the next zero : $$\arg \zeta(1/2+282.46511477 i)\approx -0.019777908$$ The point is that the orbit near this zero makes a loop at the left and with the imaginary part shortly positive before crossing the origin (note that the argument is a small negative number) ; this happens from time to time. As indicated this 'graphical error' doesn't propagate for reasons that may become clear from this thread. – Raymond Manzoni Nov 06 '15 at 22:47
  • I have the feeling that if you could make your zeta zeros counting function to count the Riemann zeta zeros perfectly, without the "non-propagating error of ±2" you are one step closer to proving the Riemann hypothesis. Why do I think that? Well it is because the Franca-Leclair approximation fits so nicely into the zeta zeros counting function. Or at least it appears to fit nicely. What I mean is that there is an integral that gives at least the first 126 zeta zeros, by combining the counting function with the Franca Leclair approximation. – Mats Granvik Nov 07 '15 at 11:40
  • @MatsGranvik: Well the repartition of the zeros itself was proved very regular (from Riemann's results) and this 'coupling' of the zeros with $\theta(t)$ (cf Backlund's proof from my last link) justifies that the counting formula works so well. The observed "graphical glitches" on the other side appear often (no dogmatic 'always'!) after or before a 'large' loop (in your case the argument variation exceeded $,2\pi,$ before the zero). At these irregular points "Gram's law" may be broken and – Raymond Manzoni Nov 08 '15 at 11:23
  • Lehmer's phenomenon may occur : two consecutive zeros will be very narrow (for example around $t=17143.8$). This may appear because the previous and next loop are both large so that the intermediate loop will be short and small (I am not excluding other behaviors).

    To prove the Riemann hypothesis wrong without leaving the critical line we only need to find a large value of $t$ such that $;Z(t):=\zeta(1/2+it),e^{i,\theta(t)};$ attains a local maximum or minimum (see the Lehmer link for more).

     – Raymond Manzoni Nov 08 '15 at 11:24
  • (the point is that this could indeed occur near these 'glitches')

    Wishing you fun in your explorations anyway. Cheers,

     – Raymond Manzoni Nov 08 '15 at 11:25
  • (correction : "(in your case the argument variation approached $2\pi$ before the zero)") – Raymond Manzoni Nov 08 '15 at 11:37
  • Ok, thanks for the links. I am merely looking at sign changes in the zeta function and the loose match between them and the failure of integral that is the Franca Leclair approximation combined with zeta zero counting function. Link to Mathematica 8 code on Pastebin: http://pastebin.com/Mg3ZHzXA The positions of the rationals in the sequence failure or success are the zeta zeros that I can't compute. Also in the code I use the Exclusions command when "n" is a zeta zero. With "loose match" I mean that it does not work always. – Mats Granvik Nov 08 '15 at 11:43
  • @MatsGranvik: Thanks for the Mma code. Correct links concerning Lehmer's phenomenon should be here and here. – Raymond Manzoni Nov 08 '15 at 14:27
  • I posted new zeta zero counting function question here: http://math.stackexchange.com/questions/2136668/prove-that-these-two-zeta-zero-counting-functions-are-essentially-the-same-when I don't know if it is really new. – Mats Granvik Feb 09 '17 at 13:49
  • @Mats Granvik: I didn't check your formula in full details (I am not sure of the $;\text{sgn}(\Im(\zeta\cdots));$ term either...) but it appears as a variant of the formula given here using the expansion of $\vartheta(t)$ proposed in this answer (this is Riemann's idea followed by proofs by Backlund, Turing and others). I would bet too that your formula becomes wrong from time to time (as for the formula here) near large 'loops' of zeta on the critical line. Wishing you fun playing with all that anyway, – Raymond Manzoni Feb 09 '17 at 23:14
  • I mentioned your name here: http://mathoverflow.net/a/261734/25104 The counting function is accurate enough to capture at least the first 10 zeta zeros numerically as a (numerical) integral, when wrapping the/your counting function with the sign function. – Mats Granvik Feb 13 '17 at 18:40
  • Thanks for the intention @MatsGranvik even if the MO thread "Explicit formula for Riemann zeros counting function" could be a better starting point for MO. I must add that these formulas use the zeta function change of sign at the zeros to detect them (more exactly the change of argument there which would work with any analytical function with nonzero derivative!) – Raymond Manzoni Feb 13 '17 at 23:49
  • i.e. using the value $t$ where $\zeta\left(\frac 12+it\right)=0$ to find a zero will of course work but will not learn us much about closed forms for the zeros! It could be more interesting to replace $\zeta$ by prime numbers or a simpler function as in the MO thread linked. Cheers, – Raymond Manzoni Feb 13 '17 at 23:57
3

Check out Andrew Odlyzko's work.His main page is here:

http://www.dtc.umn.edu/~odlyzko/doc/zeta.html

Here is a table of zeros:

http://www.dtc.umn.edu/~odlyzko/zeta_tables/

Check out this paper for algorithms:

http://www.dtc.umn.edu/~odlyzko/doc/arch/zeta.fn.supercomp.pdf

And for large zeros, this one:

http://www.dtc.umn.edu/~odlyzko/doc/zeta.10to22.pdf

Alex R.
  • 32,771
3

Assuming you mean the number n of roots $\rho$ whose imaginary parts lie between 0 and T, Riemann conjectured and von Mangoldt verified that the number is

$$n \approx\frac{T}{2\pi}\log\frac{T}{2\pi} -\frac{T}{2\pi} $$ with relative error of $O(\log T).$

There are no doubt better estimates but this is a rule-of-thumb.

daniel
  • 10,141
1

In the spirit of Raymond Manzoni's answer in combination with the Franca-LeClair asymptotic of the zeta zeros here, one can arrive at the following almost identical zeta zero counting function:

$$f(t)=\left\lfloor \frac{t \log \left(\frac{t}{2 e \pi }\right)}{2 \pi }+\frac{7}{8}\right\rfloor +\frac{1}{2} \left(-1+\text{sgn}\left(\Im\left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)\right)$$

where only the singularities are different.

The plot looks like this:

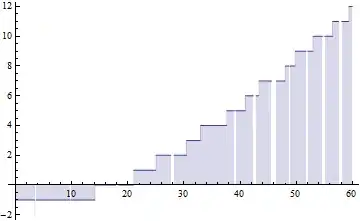
counting function

Mathematica 8 code for the plot:

(*Mathematica 8*)
Plot[(Sign[Im[Zeta[1/2 + I*t]]] - 1)/2 + 
  Floor[t/(2*Pi)*Log[t/(2*Pi*Exp[1])] + 7/8], {t, 0, 60}, 
 Filling -> 0]

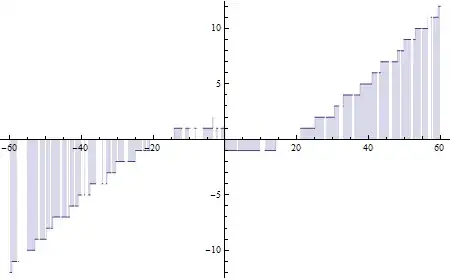
Just like Raymonds version also this counting function can be made symmetrical:

Plot[Re[(Sign[Im[Zeta[1/2 + I*t]]] - 1)/2 + 
   Floor[t/(2*Pi)*Log[t/(2*Pi*Exp[1])] + Sign[t]*7/8 + 
     If[t < 0, 2, 0]]], {t, -60, 60}, Filling -> 0]

zeta zero counting symmetry

Update 13.5.2017:

$f(t)=\frac{\Im\left(\text{log$\Gamma $}\left(\frac{1}{4}+\frac{i t}{2}\right)\right)}{\pi }+\frac{\Im\left(\log \left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)}{\pi }-\frac{t \log (\pi )}{2 \pi }+1$

$f(t)=\left\lfloor \frac{\Im\left(\text{log$\Gamma $}\left(\frac{1}{4}+\frac{i t}{2}\right)\right)}{\pi }-\frac{t \log (\pi )}{2 \pi }+1\right\rfloor +\frac{1}{2} \left(-1+\text{sgn}\left(\Im\left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)\right)+1$

$f(t)=\frac{\vartheta (t)+\Im\left(\log \left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)}{\pi }+1$

$f(t)=\left\lfloor \frac{\vartheta (t)}{\pi }+1\right\rfloor +\frac{1}{2} \left(-1+\text{sgn}\left(\Im\left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)\right)+1$

$f(t)=\left\lfloor \frac{t \log \left(\frac{t}{2 \pi \exp (1)}\right)}{2 \pi }+\frac{7}{8}\right\rfloor +\frac{1}{2} \left(-1+\text{sgn}\left(\Im\left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)\right)+1$

$f(t)=\frac{t \log \left(\frac{t}{2 \pi \exp (1)}\right)}{2 \pi }+\frac{\Im\left(\log \left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)}{\pi }+\frac{7}{8}$

Update 25.5.2017:

In the formulas above:
$\Im\left(\log \left(\zeta \left(i t+\frac{1}{2}\right)\right)\right)=\arg \left(\zeta \left(i t+\frac{1}{2}\right)\right)$

I am not sure all of the formulas are correct but they agree for the first few values I have computed.

Mats Granvik
  • 7,396