0
(*Mathematica 8 start*)
Clear[n, k, t, z, FL, NZ]
N[ZetaZero[127]]
NZ[t_] = Arg[Zeta[1/2 + I*t]]/Pi;
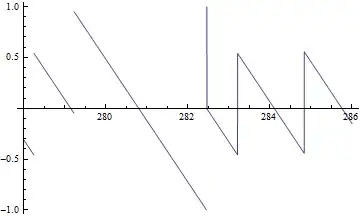
Plot[NZ[t], {t, 280, 284}]
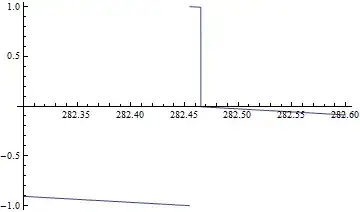
Plot[NZ[t], {t, 282.3, 282.6}]

Look at these two graphs of $$\arg(\zeta(1/2+I\cdot t))$$ around the Riemann zeta function zero 0.5 + 282.465 I:

Failure zoom out

Failure zoom in

Is it correct that close to $t=282.465$ the graph should make a jump increase of size $2$, and then should continue only slightly downwards, and then should suddenly decrease a step of almost equal to $1$? Should it be that way?

Mats Granvik
  • 7,396
  • Your question here is related to my recent question at https://math.stackexchange.com/q/4037391. By the way, what would be the advantage of the zeta zero counting function that you were attempting to derive (which last I recall you could only evaluate using NIntegrate) over formulas such as $N_0(T)=1+\frac{\vartheta(T)}{\pi}+\frac{\arg\left(\zeta\left(\frac12+i,T\right)\right)}{\pi}$? Would your formula not exhibit the same anomalies as this formula near Gram points that violate Gram's law? – Steven Clark Feb 25 '21 at 23:10
  • I seem to recall now you were working on a formula for calculating the location of the zeta zeros, so perhaps my question in the previous comment was misguided and I should really be asking if violations of Gram's law causes problems with your algorithm when attempting to find the location of a zeta zero in the neighborhood of a Gram point where Gram's law is violated.. – Steven Clark Feb 26 '21 at 00:36
  • It might not be feasible but if you could make an integrable approximation of the zeta zero counting function it would give a formula for the zeta zeros. More exceptions like this one here (in my question) are found here: https://oeis.org/A153815 Notice also that any solution to the integral of Log[Zeta[s]] (in the critical strip) would be interesting with regards to the Riemann hypothesis as pointed out here: https://mathoverflow.net/a/57944/25104 – Mats Granvik Feb 26 '21 at 14:22

1 Answers1

5

The argument jumps by $\pi$ at each zero because the curve $\zeta(\frac12+it)$ passes right through the origin. (With the principal argument the jump will be upwards or downwards according to whether the curve passes from the lower half-plane to the upper one, or vice versa).

The large jump by $2\pi$ just before the zero is just caused by normalization of the argument to fall within the standard interval $(-\pi,\pi]$. It shows that the curve crosses the negative real axis shortly before the zero at 282.465.

Note that the almost stable downwards slope of the graph between the jumps is because what you're really plotting is minus the the Riemann-Siegel theta function, plus $\pi$ times the number of critical zeroes below $t$, modulo $2\pi$, and the theta function is quite smooth for such large $t$.

hmakholm left over Monica
  • 286,031