Generalization of the law of tangents for a cyclic quadrilateral

Question

The law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposing sides.

Let $a$, $b$, and $c$ be the lengths of the three sides of a triangle, and $\alpha$, $\beta$ and $\gamma$ be the angles opposite those three respective sides. The law of tangents states that

$$\frac{\tan\frac12(\alpha-\beta)}{\tan\frac12(\alpha+\beta)}=\frac{a-b}{a+b}\tag{1}$$

The law of tangent can be used in any case where two sides and the included angle, or two angles and a side, are known.

Although Viète gave us the modern version of the law of tangents, it was Fincke who stated the law of tangents for the first time and also demonstrated its application by solving a triangle when two sides and the included angle are given (see Wu - The Story of Mollweide and Some Trigonometric Identities)

A proof of the law of tangent is provided by Wikipedia (see here).

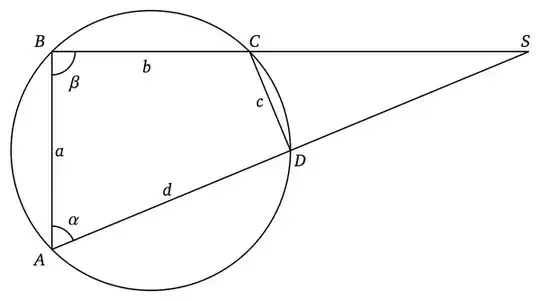
Generalization. Let $a$, $b$, $c$ and $d$ be the sides of a cyclic convex quadrilateral. Let $\angle{DAB}=\alpha$ and $\angle{ABC}=\beta$, then the following identity holds

$$\frac{\tan\frac12(\alpha-\beta)}{\tan\frac12(\alpha+\beta)}=\frac{(a-c)(b-d)}{(a+c)(b+d)}\tag{2}$$

Proof. Using the sum-to-product formulas we can rewrite the left-hand side of $(2)$ as follows

$$\frac{\tan\frac12(\alpha-\beta)}{\tan\frac12(\alpha+\beta)}=\frac{\sin\frac12(\alpha-\beta)\cos\frac12(\alpha+\beta)}{\cos\frac12(\alpha-\beta)\sin\frac12(\alpha+\beta)}=\frac{\sin{\alpha}-\sin{\beta}}{\sin{\alpha}+\sin{\beta}}.$$

The area of a cyclic quadrilateral can be expressed as $\Delta=\frac12(ad+bc)\sin{\alpha}$ (see $(12)$ at Killing three birds with one stone) and similarly for the other angles. Then substituting, simplifying and factorizing we have

$$\begin{align*}\frac{\tan\frac12(\alpha-\beta)}{\tan\frac12(\alpha+\beta)}&=\frac{\frac{2\Delta}{ad+bc}-\frac{2\Delta}{ab+cd}}{\frac{2\Delta}{ad+bc}+\frac{2\Delta}{ab+cd}}=\frac{ab-ad+cd-bc}{ab+ad+cd+bc}=\frac{(a-c)(b-d)}{(a+c)(b+d)}\end{align*}.$$

$\square$

The formula $(2)$ reduces to the law of tangent for a triangle when $c=0$.

A related result can be found at A generalization of Mollweide's formula (rather Newton's).

Crossposted at MO.

Question: Is this generalization known?

A historical correction: Fincke was not the first to publish the law of tangents. It was actually Ibn Muadh who first described it in the 11th century. See the discussion at HSMSE.

Answer 1

The Usual Law of Tangents

Applying the formulae for the Sum of Sines and the Sum of Cosines, we get $$ \begin{align} \frac{\sin(A)+\sin(B)}{\cos(A)+\cos(B)} &=\frac{2\sin\left(\frac{A+B}2\right)\cos\left(\frac{A-B}2\right)}{2\cos\left(\frac{A+B}2\right)\cos\left(\frac{A-B}2\right)}\\[6pt] &=\tan\left(\tfrac{A+B}2\right)\tag1 \end{align} $$ Substituting $B\mapsto-B$ in $(1)$ and then dividing by $(1)$ gives $$ \frac{\sin(A)-\sin(B)}{\sin(A)+\sin(B)}=\frac{\tan\left(\frac{A-B}2\right)}{\tan\left(\frac{A+B}2\right)}\tag2 $$ If we let $a$ and $b$ be the sides opposite angles $A$ and $B$ respectively, the Law of Sines leads to $$ \frac{a-b}{a+b}=\frac{\sin(A)-\sin(B)}{\sin(A)+\sin(B)}\tag3 $$

Equating $(2)$ and $(3)$, we get the Law of Tangents $$ \frac{a-b}{a+b}=\frac{\tan\left(\frac{A-B}2\right)}{\tan\left(\frac{A+B}2\right)}\tag4 $$ where $a$ and $b$ are the sides of a triangle opposite angles $A$ and $B$ respectively.

---

Inscribed Generalization

The power of the point $S$ is equal to both $\overline{SA}\,\overline{SD}=\overline{SB}\,\overline{SC}$; therefore, $$ \frac{\overline{SA}}{\overline{SB}}=\frac{\overline{SC}}{\overline{SD}}\tag5 $$ and since $\angle ASB=\angle CSD$, SAS says that $$ \triangle ASB\simeq\triangle CSD\tag6 $$ Therefore, $$ \frac{\overline{SA}}{\overline{SC}}=\frac{\overline{SB}}{\overline{SD}}=\frac ac\tag7 $$ Thus, we have $$ \begin{align} b&=\overline{SB}-\overline{SC}=\overline{SB}-\overline{SA}\frac ca\tag{8a}\\[6pt] d&=\overline{SA}-\overline{SD}=\overline{SA}-\overline{SB}\frac ca\tag{8b} \end{align} $$ From $(8)$, we can solve $$ \begin{align} \overline{SA}&=a\frac{ad+bc}{a^2-c^2}\tag{9a}\\[3pt] \overline{SB}&=a\frac{ab+cd}{a^2-c^2}\tag{9b} \end{align} $$ Now we are ready to apply the usual Law of Tangents from $(4)$: $$ \begin{align} \frac{\tan\left(\frac{\alpha-\beta}2\right)}{\tan\left(\frac{\alpha+\beta}2\right)} &=\frac{\overline{SB}-\overline{SA}}{\overline{SB}+\overline{SA}}\tag{10a}\\ &=\frac{(ab+cd)-(ad+bc)}{(ab+cd)+(ad+bc)}\tag{10b}\\[6pt] &=\frac{(a-c)(b-d)}{(a+c)(b+d)}\tag{10c} \end{align} $$