1

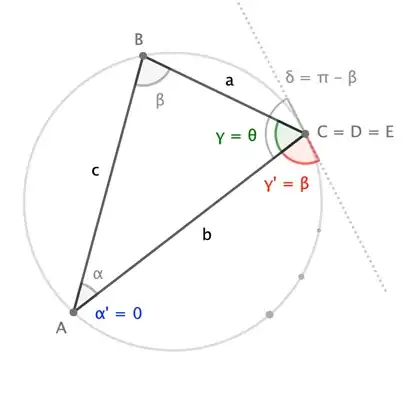
Note that as with Mollweide's Formulas, this version for a cyclic quadrilateral not only relates the four sides to the four angles, but also includes the angle between the diagonals. It is not clear to me if this expression generalizes the Mollweide's Formulas or Newton's Formulas (which is my intention), so my question is: does the Mollweides's Formula (or Newton's version) follows from the relation in the image?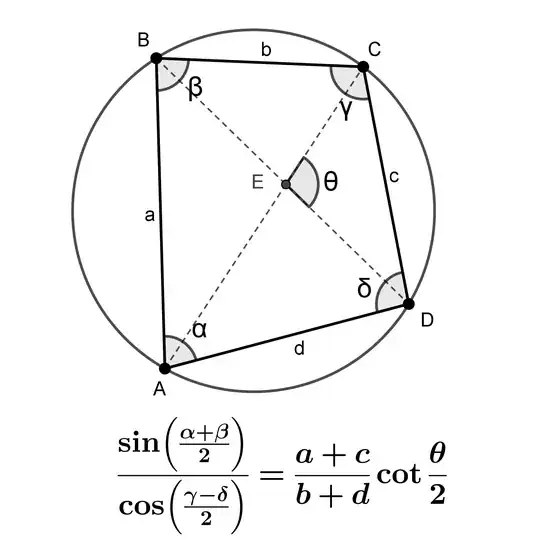enter image description here

Jean-Claude Arbaut
  • 23,277
Emmanuel José García
  • 807
  • 2
    Interesting question. However, rather than making people visit other sites just to understand what you're even talking about, please include the specific formulas of interest in the body of your question. Cheers! – Blue Jan 10 '22 at 17:40
  • @Blue, unfortunately I won't be able to do that for long, so if anyone can edit the question to make it clearer, please feel free to do so. – Emmanuel José García Jan 10 '22 at 18:16
  • It really seems that this formula cannot be adapted to a triangle. – Emmanuel José García Jan 14 '22 at 17:58
  • "It really seems that this formula cannot be adapted to a triangle." Actually, if you move $D$ to coincide to $C$, then the formula reduces to equation (3) on Wolfram's "Newton's Formulas" entry (with some labeling adjustments), so the identity does in fact generalize Newton. – Blue Jan 14 '22 at 18:53
  • 1
    I have never been so glad to be wrong. I love you Blue. This is another example of what the half angle formulas can do for us. The following link contains my proof of the -now confirmed- generalization. Link:https://geometriadominicana.blogspot.com/2022/01/generalization-of-mollweides-formulas.html?spref=fb&fbclid=IwAR2rSc65k1queRRQulY6S97Z1KLhwCoqv79B4fMzhkqPj2xd8DMuoU9xcno – Emmanuel José García Jan 16 '22 at 14:55
  • A related question has been posted here: https://math.stackexchange.com/questions/4404991/generalization-of-the-law-of-tangents-for-a-cyclic-quadrilateral – Emmanuel José García Apr 19 '22 at 13:07

1 Answers1

1

Anticipating reducing the formula to one of Newton's, rename elements of the figure as shown:

enter image description here

That is, angles $\alpha$ and $\gamma$ have been sub-divided into $\alpha+\alpha'$ and $\gamma+\gamma'$, and the segment labels have been scrambled: $a:=|BC|$, $b := |AD|$, $c:=|AB|$, $d:=|CD|$. Note that $\delta = \pi-\beta$ (as $\beta$ and $\delta$ are inscribed angles subtending opposing arcs). With these changes, the formula in question becomes

$$\frac{c+d}{a+b}\;\cot\frac12\theta = \frac{\sin\frac12(\alpha+\alpha'+\beta)}{\cos\frac12(\gamma+\gamma'-(\pi-\beta))} \to \frac{c+d}{a+b}\;\cot\frac12\theta = \frac{\sin\frac12(\alpha+\alpha'+\beta)}{\sin\frac12(\gamma+\gamma'+\beta)} \tag{1}$$

Now, if we slide vertex $D$ along the circle to coincide with $C$ (so that $E$ does as well), we find that $\alpha'$ and $d$ shrink to nothing; $\gamma'$ and $\theta$ adjust to match $\beta$ and $\gamma$, respectively; and $\beta$ and $\delta$ don't change at all.

enter image description here

So, $(1)$ becomes

$$\frac{c+0}{a+b}\;\cot\frac12\gamma = \frac{\sin\frac12(\alpha+0+\beta)}{\sin\frac12(\gamma+\beta+\beta)} \quad\to\quad \frac{c}{a+b}\;\cot\frac12\gamma = \frac{\sin\frac12(\alpha+\beta)}{\sin\frac12(\gamma+2\beta)} \tag2$$

Since $\alpha+\beta+\gamma=\pi$, we have $$\alpha+\beta=\pi-\gamma \qquad\qquad\gamma+2\beta = \pi-(\alpha-\beta)$$ whence $(2)$ becomes $$\frac{c}{a+b}\;\frac{\cos\frac12\gamma}{\sin\frac12\gamma} = \frac{\sin\left(\frac\pi2-\frac12\gamma\right)}{\sin\left(\frac\pi2-\frac12(\alpha-\beta)\right)} = \frac{\cos\frac12\gamma}{\cos\frac12(\alpha-\beta)} \tag3$$ and we can write

$$\frac{a+b}{c} = \frac{\cos\frac12(\alpha-\beta)}{\sin\frac12\gamma} \tag{$\star$}$$

which is formula $(3)$ on MathWorld's "Newton's Formulas" entry. $\square$

Blue
  • 75,673