1

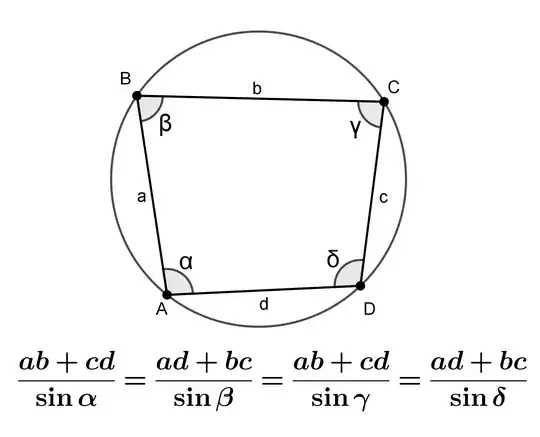
I have been exploring possibilities with the Half Angle Formulas for almost two years (maybe not the ones you have in mind, see link below) and it never ceases to amaze me. Yesterday, playing with the version for a cyclic quadrilateral, I found this extension of the Law of Sines. The proof is pretty simple, but let's be honest, did you know about it? Because I do not. Every day I am more convinced that the HAF are as or more fundamental than the Law of Cosines or the Pythagorean Theorem, which, incidentally, can be derived from them. I hope they will soon enjoy the same popularity.

In a convex cyclic quadrilateral the interior angles are formed by line segments that are the sides. By making $d = 0$, not only the side $d$ disappears, the angles $\alpha$ and $\delta$ also disappear forming another angle, and leaving $\beta$ and $\gamma$. So from the relation of the image you take the terms that contain $\beta$ and $\gamma$: $(ad + bc) / \sin\beta = (ab + cd) / \sin\gamma$. Making $d = 0$, the expression reduces to $bc / \sin\beta= ab / \sin\gamma$, finally, multiplying both terms by $1 / b$ you get $c / \sin\beta = a / \sin\gamma$, which is the Law of Sines for a triangle.

Link: https://geometriadominicana.blogspot.com/2020/06/another-proof-for-two-well-known.html

Any reference?

enter image description here

ACB
  • 3,713
Emmanuel José García
  • 807
  • @MyMolecules It is clear in the post I am asking for references – Emmanuel José García Dec 28 '21 at 16:20
  • The link I have provided are the formulas from which I have derived the generalization. I want to know if this generalization is known. – Emmanuel José García Dec 28 '21 at 16:50
  • These are trivial formulae. Area of cyclic quadrilateral = $0.5(ab+cd)\sin \beta = 0.5(ad+bc)\sin \alpha$. And $\sin \alpha = \sin \gamma$, $\sin \beta = \sin \delta$. Also, I don't see point of mentioning half-angle formulae. – MyMolecules Dec 28 '21 at 16:54
  • So what? I said that in my post. I am asking for references. The Law of Sines for a triangle is a corollary of this relationship. – Emmanuel José García Dec 28 '21 at 16:56
  • 2
    I'm sure someone who knows will answer. It will be a good idea to explain in your post, how the law of sines for triangle follows from above formulas. – MyMolecules Dec 28 '21 at 16:59
  • A related question has been posted here: https://math.stackexchange.com/questions/4404991/generalization-of-the-law-of-tangents-for-a-cyclic-quadrilateral – Emmanuel José García Apr 19 '22 at 13:09

0 Answers0