Disclaimer - this is not an independent answer!
I have transformed the geometric construction in Intelligenti pauca's excellent answer into algebra using homogeneous coordinates. From that,
I observed the center of inellipse can be expressed as a weighted sum of vertices ($*5$) and the weights can be computed from the areas of various triangles associated with the pentagon.
In the answer below, I have thrown away the uninspiring algebra and proved the most "unexpected" relation ($*4$) by more elementary means (trigonometry).
- For any $P = (x_p,y_p), Q = (x_q,y_q)$ in the plane, let $$[PQ] \stackrel{def}{=} x_py_q - x_qy_p$$ Please note that $[PQ] = -[QP]$ and geometrically, it is twice the signed area of a triangle with vertices at $P,Q$ and origin $O$.
- For any $P, Q, R$ in the plane, let
$$[PQR] \stackrel{def}{=} [PQ] + [QR] + [RQ]$$
Please note that $[PQR] = [QRP] = [RPQ]$ and geometrically, it is twice the signed area of a triangle with vertices at $P,Q,R$.
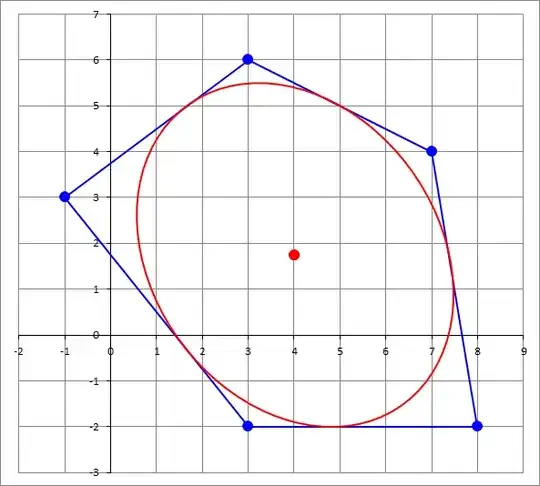
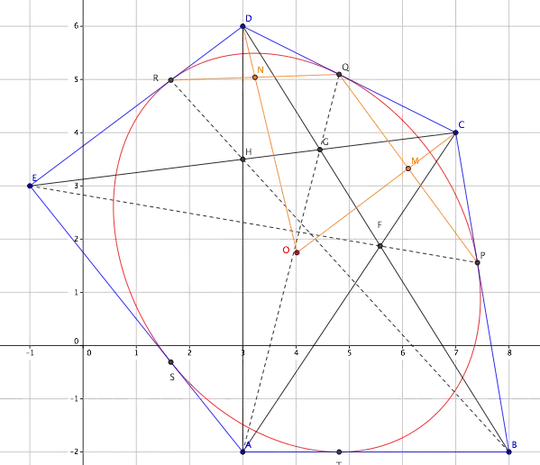
Let $A,B,C,D,E$ be the vertices of a convex pentagon (ordered counterclockwisely). Let $G$ be its center of mass and $K$ be the center of its in-ellipse.
Pick any point $P$ within the pentagon. Cut the pentagon at $P$ to form 5 triangles. We can compute $G$ as the area weighted average of the centroid of the $5$ triangles:
$$3G = \frac{\sum_{cyc} [ABP] (A+B+P)}{\sum_{cyc}[ABP]} \tag{*1}$$
RHS of $(*1)$ can be viewed as a rational function in coordinates of $P$. Since this is valid for all points within the pentagon, it is valid for all points in the plane. In particular, if we substitute $P$ by origin $O$ in $(*1)$, we obtain
$$3G = \frac{\sum_{cyc}[AB](A+B)}{\sum_{cyc}[AB]}\tag{*2}$$
Substitute $P$ by $K$ in $(*1)$ and combine with $(*2)$, we can express $K$ as a weighted sum of vertices:
$$K = \frac{\sum_{cyc}[AB](A+B)}{\sum_{cyc}[AB]} - \frac{\sum_{cyc} [ABK] (A+B)}{\sum_{cyc}[ABK]}\tag{*3}$$
It turns out the ratios among $[ABK], [BCK], \ldots$ can be computed from the areas of various triangles associated with the pentagon. More precisely, let
$$
\lambda_A = [ABE][ACD],\;\;
\lambda_B = [BCA][BDE], \ldots $$
(definition of $\lambda_C,\lambda_D,\lambda_E$ can be derived from that of $\lambda_A$ by cyclic permuting the vertices). We have
$$\frac{[ABK]}{\lambda_A+\lambda_B}
= \frac{[BCK]}{\lambda_B+\lambda_C}
= \frac{[CDK]}{\lambda_C+\lambda_D}
= \frac{[DEK]}{\lambda_D+\lambda_E}
= \frac{[EAK]}{\lambda_E+\lambda_A}\tag{*4}$$
Combine these with $(*3)$, we obtain a formula we seek.
$$
\bbox[border: 1px solid blue;padding: 1em;]{
K = \frac{\sum_{cyc}[AB](A+B)}{\sum_{cyc}[AB]} - \frac{\sum_{cyc} (\lambda_A + \lambda_B) (A+B)}{2\sum_{cyc}\lambda_A}}\tag{*5}$$
What's remain is to justify $(*4)$. Since under affine transform, the ratio of areas remains invariant. It suffices to verify $(*4)$ when the inellipse is the unit circle centered at origin and $A$ lies on the +ve $x$-axis.
Let $A_1,B_1,C_1,D_1,E_1$ be points on the inellipse touching the pentagon edges $CD$, $DE$, $EA$, $AB$, $BC$ respectively. Let
$$2\alpha = \angle C_1OD_1, 2\beta = \angle D_1OE_1, 2\gamma = \angle E_1OA_1, 2\delta = \angle A_1OB_1, 2\epsilon = \angle B_1OC_1$$
It is not hard to see the vertices are located at
$$
\begin{align}
A &= \frac{1}{\cos\alpha}(1, 0)\\
B &= \frac{1}{\cos\beta}(\cos(\alpha+\beta),\sin(\alpha+\beta))\\
C &= \frac{1}{\cos\gamma}(\cos(\alpha+2\beta+\gamma),\sin(\alpha+2\beta+\gamma))\\
D &= \frac{1}{\cos\delta}(\cos(\alpha+2\epsilon+\delta),-\sin(\alpha+2\epsilon+\delta))\\
E &= \frac{1}{\cos\epsilon}(\cos(\alpha+\epsilon),-\sin(\alpha+\epsilon))
\end{align}$$
With this, it is not hard to verify
$$[AB] = \tan\alpha + \tan\beta, [BC] = \tan\beta + \tan\gamma,\ldots$$
Furthermore,
$$
\begin{align}[ABE]
&= (\tan\alpha + \tan\beta)(\tan\alpha + \tan\epsilon)\sin(2\alpha)\\
&= 2\frac{\sin(\alpha+\beta)\sin(\alpha+\epsilon)}{\cos\alpha\cos\beta\cos\epsilon}\sin\alpha\\
[ACD]
&= (\tan\gamma + \tan\delta)\left(1 - \frac{\cos(\alpha+2\beta+2\gamma)}{\cos\alpha}\right)\\
&= 2\frac{\sin(\gamma+\delta)}{\cos\alpha\cos\gamma\cos\delta}
(\sin(\alpha+\beta+\gamma)\sin(\beta+\gamma)\\
&= 2\frac{\sin(\gamma+\delta)\sin(\delta+\epsilon)\sin(\beta+\gamma)}{\cos\alpha\cos\gamma\cos\delta}
\end{align}$$
This leads to
$$\lambda_A = [ABE][ACD] = 4\tan\alpha \prod_{cyc}\frac{\sin(\alpha+\beta)}{\cos\alpha}$$
There are similar formulas for $\lambda_B,\lambda_C$ and at the end, we get
$$\frac{\lambda_A + \lambda_B}{[AB]} = \frac{\lambda_A + \lambda_B}{\tan\alpha + \tan\beta} = 4\prod_{cyc}\frac{\sin(\alpha+\beta)}{\cos\alpha}$$
Notice RHS is invariant under cyclic permutation of vertices. This justifies $(*4)$ in this special case and hence in general.