Note: originally I had misunderstood “diameter” to refer to mean “axis”. My original answer was based on that, and on constructing a counter-argument to that. I've completely rewritten my answer since.
does it exist always at least one diameter of the ellipse such that the line containing it divides the pentagon's perimeter and/or area in equal parts?
Yes. Assume you start with any oriented line through the center of the ellipse. It will divide the whole perimeter $s$ into a part $\lambda s$ on the positive side and a part $(1-\lambda)s$ on the negative side. Now as you rotate the line, $\lambda$ will change. Once you have rotated the line by $180°$ the roles of $\lambda$ and $1-\lambda$ have switched. So if you had more than half the perimeter on one side to begin with, i.e. $\lambda>\frac12$, then you have less than half in the end. Since the change in perimeter is continuous (no jumps), it has to be exactly half somewhere in between. This follows from the intermediate value theorem.
Exactly the same argument can be made for the area: rotating the line by $180°$ exchanges any larger and smaller side you might have initially, so they have to even out somewhere in between.
Actually the argument doesn't use the inscribed ellipse at all. Any point inside the pentagon would serve as the point around which you rotate the line. Through any point you can find at least one line which divides the perimeter in half, and one line which divides the area in half.
Looking at your “and/or” wording I realize that you might also be interested in a line which cuts both perimeter and area in half at the same time. And there it might be conceivable that the center of the inscribed ellipse plays a relevant role. So let's just use the fairly arbitrary pentagon I define below (scroll down for actual coordinates), and look at that.
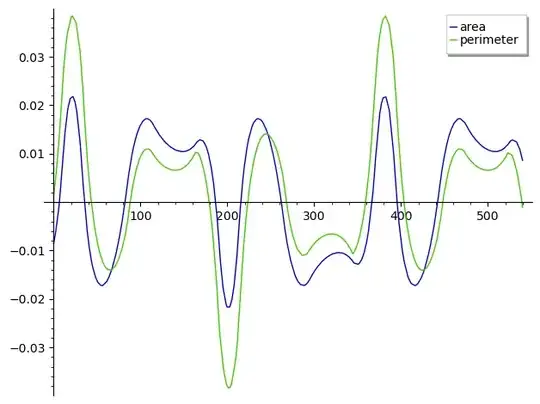
The $x$ axis of this plot has the angle of the diameter line, in degrees. You will notice a $360°$ periodicity, and you will also notice that after $180°$ you get the same shape flipped. The vertical axis is ratio of area or perimeter on the one side of the line divided by total area or perimeter, minus $\frac12$. So it is the excess over the exact half, in units of ratio of the total. A zero in the graph means equal area or perimeter in both halfs, for that specific angle.
As you can easily see, the two different lines in the plot don't cross the $x$ axis in the same points. They are not zero for the same angle. You don't get a line which cuts both perimeter and angle in half at the same time.
I have not found any proof of the initial statement of uniqueness of the inscribed ellipse, so I would appreciate any reference as well.
For that aspect I'll retain parts of my original answer, and construct the inscribed ellipse for a specific set of pentagon corners as a demonstration. That's probably not the kind of proof you want, but since my original answer already had an upvote I assume that part might have been useful nonetheless, to you or some other readers.
My specific pentagon, chosen arbitrarily but without resorting to a random number generator, is this:
$$
A=\begin{pmatrix}0\\0\end{pmatrix}\quad
B=\begin{pmatrix}6\\0\end{pmatrix}\quad
C=\begin{pmatrix}10\\4\end{pmatrix}\quad
D=\begin{pmatrix}5\\7\end{pmatrix}\quad
E=\begin{pmatrix}1\\4\end{pmatrix}
$$
I have a background in projective geometry so I will use homogeneous coordinates to describe points, and cross products to compute lines. For example the first edge of the pentagon I compute as
$$
a \sim A\times B = \begin{pmatrix}0\\0\\1\end{pmatrix} \times
\begin{pmatrix}6\\0\\1\end{pmatrix} = 6\begin{pmatrix}0\\1\\0\end{pmatrix}
\qquad a = \begin{pmatrix}0\\1\\0\end{pmatrix}
$$
which represents the line $0x+1y+0=0$ or written more simply $y=0$. I'm getting rid of the factor $6$ to keep things simple, and I'm using the variable $a$ to refer to this already simplified vector. In the same way I get
$$
a = \begin{pmatrix}0\\1\\0\end{pmatrix} \quad
b = \begin{pmatrix}-1\\1\\6\end{pmatrix} \quad
c = \begin{pmatrix}-3\\-5\\50\end{pmatrix} \quad
d = \begin{pmatrix}3\\-4\\13\end{pmatrix} \quad
e = \begin{pmatrix}4\\-1\\0\end{pmatrix}
$$
Quick reminder, using $d$ as an example with fewer zeros, that vector describes the line $3x-4y+13=0$. OK, now we want the conic. And we want to compute it in the dual world, as a conic tangent to 5 lines not a conic passing through 5 points. We start by forming degenerate conics of rank 2 which each correspond to a pair of points, and we describe these conics as symmetric matrices.
$$
M_1 = (a\times b)(c\times d)^T + (c\times d)(a\times b)^T =
\begin{pmatrix}1620&1134&297\\1134&0&189\\297&189&54\end{pmatrix}
\\
M_2 = (a\times c)(b\times d)^T + (b\times d)(a\times c)^T =
\begin{pmatrix}3700&1550&161\\1550&0&93\\161&93&6\end{pmatrix}
$$
Note that these cross products represent intersections of lines, so for some of them we might have used our original corner points instead. But I decided to not do that for the sake of consistency, and let my computer algebra system deal with the slightly bigger numbers instead. $M_1$ and $M_2$ already have $a$ through $d$ as tangents. Now we want a linear combination of the two which has $e$ as a tangent as well:
$$
M \sim (e^TM_2e)M_1 - (e^TM_1e)M_2 =
134784\begin{pmatrix}100&200&83\\200&0&54\\83&54&18\end{pmatrix}\\
M = \begin{pmatrix}100&200&83\\200&0&54\\83&54&18\end{pmatrix} \\
a^TMa = b^TMb = c^TMc = d^TMd = e^TMe = 0
$$
So $M$ describes the ellipse as a dual conic, as a collection of tangent lines, and our lines $a$ through $e$ are indeed tangent as the last equation shows. You can use that to compute the homogeneous coordinates of its center, which is the pole of the line at infinity.
$$
K = M\cdot\begin{pmatrix}0\\0\\1\end{pmatrix}
= \begin{pmatrix}83\\54\\18\end{pmatrix}
$$
which corresponds to $K=\left(\frac{83}{18},\frac{54}{18}\right)$ as the dehomogenized coordinates of the center. So that's the point all your diameters will pass through.
If you want the ellipse as a primal conic of incident points, instead of a dual conic of tangent lines, you can take the adjunct matrix.
$$
N = \operatorname{adj}(M) = \begin{pmatrix}
-2916 & 882 & 10800 \\
882 & -5089 & 11200 \\
10800 & 11200 & -40000
\end{pmatrix} \\
-(x,y,1)\cdot N\cdot\begin{pmatrix}x\\y\\1\end{pmatrix} =
2916x^2 + 5089y^2 - 1764xy - 21600x - 22400y + 40000
$$
So that last polynomial being zero is the characterization of your ellipse as a set of points. Back to your question:
I have not found any proof of the initial statement of uniqueness of the inscribed ellipse, so I would appreciate any reference as well.
It's not exactly a proof, but the approach above demonstrates how you can get such an ellipse given 5 lines. The approach handles one of the lines different from the others, but making a different choice there only results in a change to every coefficient of your equation by the same factor, and such a change has no geometric relevance. Note that the case where 3 of your lines are concurrent is special, and typically excluded explicitly.
You might augment intuition by observing that the equation of a conic has six coefficients. But since scaling the whole equation changes nothing, there is only five real degrees of freedom. Each line fixes one degree of freedom, because the homogeneous coordinate vector of the line itself has 3 coordinates, 2 geometric degrees of freedom after ignoring common factors, but as you can move a tangent along a conic without changing the conic, only 1 of these degrees is actually contributing to defining the conic. All this degree-counting shows (if done more rigurously) that there can't be an infinite collection of conics satisfying your 5 tangencies. But it doesn't show that you don't have a couple of distinct solutions.
Also note that the above construction is dual to the one of a conic through 5 points. So if you accept the uniqueness of one, the uniqueness of the other could be deduced from that duality. Whether you are more at home with conics defined by 5 points is unclear, though.
