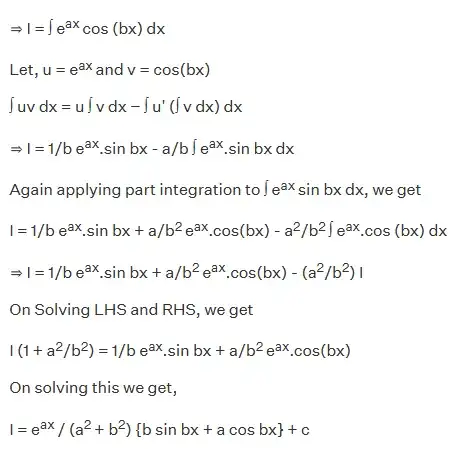0

I have this improper integral =

\begin{equation} \int_{0}^{\infty}e^{-ax}\cos x dx \end{equation}

I need to find for what a-value the integral will have a maximum value. a of course has to be: \begin{equation} a>0 \end{equation} I have tried differentiating the integral and putting it equal to zero to find critical values and then solve for a, but all I get is an expression 0 = 0, which really doesn't help me.

Johnny Dang
  • 19

2 Answers2

1

\begin{equation} \int_{0}^{\infty}e^{-ax}\cos x dx \end{equation}

You can use Laplace Transformation:

\begin{equation} \int_{0}^{\infty}e^{-st}\cos{bt}dt =\frac{s}{s^2+b^2} \end{equation}

You can substitute values: $s = a, b = 1$

$$\begin{align*} f(a) = \frac{a}{a^2+1} \end{align*}$$

Now, You want the value of $a$ for which $f(a)$ is max.

Differentiate the function and equate to zero: $$\begin{align*} f'(a)=\frac{d}{da}(\frac{a}{a^2+1}) = 0\\ =\frac{1-a^2}{(a^2+1)^2} = 0\\ \implies a =±1 \end{align*}$$

You can find the maximum value of is @ $a=1$ which is $f(a=1) = 0.5$

  • Laplace Transform of $\cos{bt}$

Consider, $\cos{bt}=\operatorname{Re}\{e^{-ibt}\}$, $$ \int_0^\infty e^{-at}\cos(bt)\,dt= \operatorname{Re}\int_0^\infty e^{-(a+ib)t}\,dt= \operatorname{Re}\left[-\frac{e^{-zt}}{z}\right]_0^\infty= $$ $$ \operatorname{Re}\left\{\frac{1}{z}\right\}= \operatorname{Re}\left\{\frac{a-ib}{||z||^2}\right\}= \frac{a}{a^2+b^2}. $$

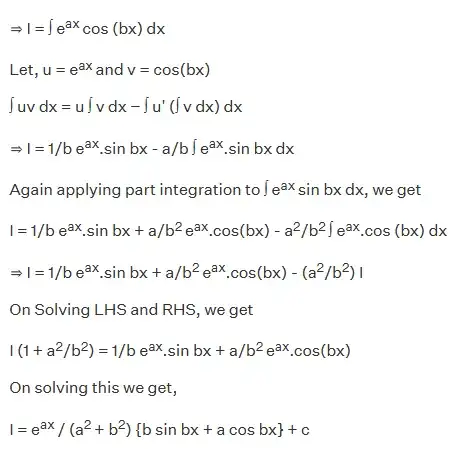
enter image description here

You can substitute your values:

As $x\to\infty$ it $\to0$

  • is it possible to do without laplace transform? – Johnny Dang Sep 30 '21 at 15:32
  • @JohnnyDang Yes! I could remember the integration of question You can integrate the above-using integration parts or product rule: You can refer this as $x \to\infty$ it will be zero because $e^{-ax}$ so just values of integration at $x=0$ will have to be checked> I'll try to add in the above answer may take time. –  Sep 30 '21 at 15:43
  • Hm, i want to find the value for a that makes the integral the max value. And a has to be greater than 0 – Johnny Dang Sep 30 '21 at 15:58
0

define: $$I=\int_0^\infty e^{-ax}\cos(x)dx\qquad J=\int_0^\infty e^{-ax}\sin(x)dx$$ then: $$K=I+iJ=\int_0^\infty e^{-ax} e^{ix}dx=\int_0^\infty e^{(i-a)x}dx$$ $$I=\Re(K)$$ now $K$ should be very easy to solve, multiplying by the complex conjugate of the bottom yields: $$K=\frac{a+i}{a^2+1}$$ $$I=\Re(K)=\Re\left(\frac{a+i}{a^2+1}\right)=\frac{a}{a^2+1}$$ and conveniently you simultaneously work out the value of $J$

Henry Lee
  • 12,215