Is a cylindroid a manifold with corners?

Question

First of all to follows we remember some elementary definitions and results about manifolds.

Definition

A function $f$ defined in a subset $S$ of $\Bbb R^k$ is said of class $C^r$ if it can be extended to a function $\phi$ (said $C^r$-extension) that is of class $C^r$ in a open neighborhood of $S$.

Lemma

If $f$ is a function defined in a subset $S$ of $\Bbb R^n$ such that for any $x\in S$ there exist a function $f_x$ defined in a neighborhood of $x$ that is of class $C^r$ and compatible with $f$ on $U_x\cap S$ then $f$ is of class $C^r$.

Lemma

If $U$ is an open set of $H^n_k:=\Bbb R^{n-k}\times[0,+\infty)^k$ for any $k\le n$ then the derivatives of two different extensions $\phi$ and $\varphi$ of a $C^r$-function $f$ agree in $U$.

Definition

A $k$-manifold with boundary/corners in $\Bbb R^n$ of calss $C^r$ is a subspace $M$ of $\Bbb R^n$ whose points have a neighborhood $V$ in $M$ that is the immage of a homeomorphism $\phi$ of calss $C^r$ defined an open set $U$ of $\Bbb R^k$ or of $H^k_1/H^k_m$ and whose derivative has rank $k$.

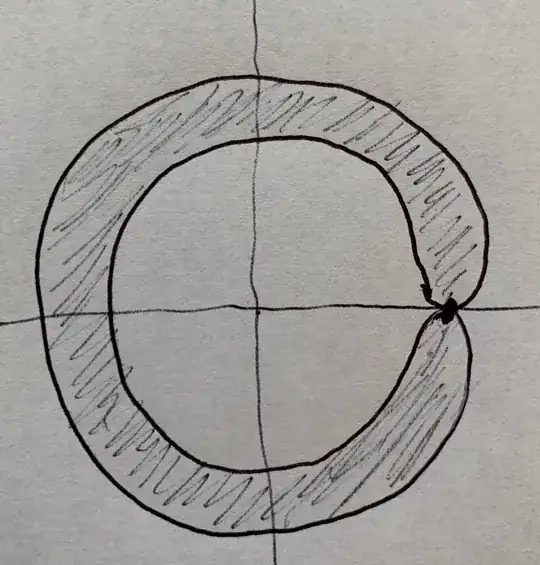
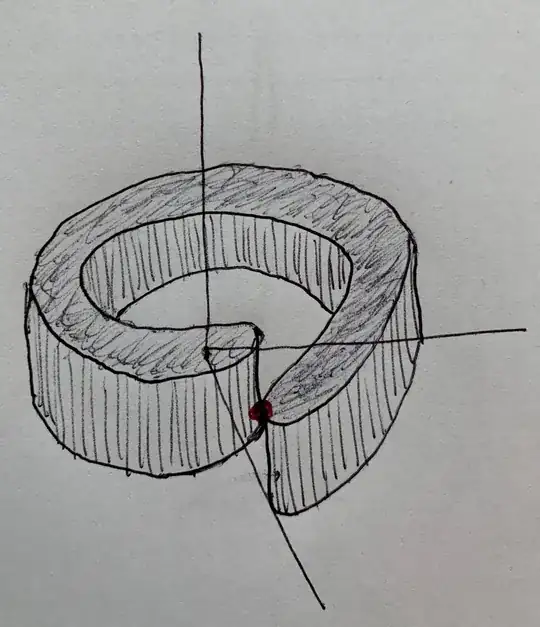
So now let be $M$ a $(n-1)$-manifold with boundary of class $C^r$ in $\Bbb R^n$ and thus let be $\gamma$ a injective curve defined in the unit interval $I:=[0,1]$ such that $\gamma(0)=0$ and such that the unit tangent vector not lies -for each $t\in I$- to the tangent space at any point of $M$. So we call cylindroid $C$ of trajectory $\gamma$ and of section $M$ the set $$ C:=\bigcup_{t\in I}\big(M+\gamma(t)\big) $$ that is obtained moving along $\gamma$ the points of $M$. Click here to see an example. So if $\xi\in C$ then there exist a coordinate patch $\alpha:U\rightarrow V$ and $t\in I$ such that $$ \xi=\alpha(x)+\gamma(t) $$ for any $x\in U$ and thus let be $\phi$ the function from $U\times I$ to $\Bbb R^n$ defined through the equation $$ \phi(x,t):=\alpha(x)+\gamma(t) $$ for any $(x,t)\in U\times I$ and then we prove that any restriction of this function is a coordinate patch about $\xi$. So we observe that the immage of $\phi$ is open in $C$: indeed the immage $V$ of $\alpha$ is an open set of $M$ so that there exist an open set $W$ of $\Bbb R^n$ whose intersection with $M$ is $V$ and so remembering that the translation is a bijection we observe that $$ \phi[U\times I]=\bigcup_{t\in I}\big(V+\gamma(t)\big)=\bigcup_{t\in I}\Big((W\cap M)+\gamma(t)\Big)=\bigcup_{t\in I}\Big(\big(W+\gamma(t)\big)\cap\big(M+\gamma(t)\big)\Big)=\\ \Biggl(\bigcup_{t\in I}\big(W+\gamma(t)\big)\Biggl)\cap\Biggl(\bigcup_{t\in I}\big(M\cap\gamma(t)\big)\Biggl)=\Biggl(\bigcup_{t\in I}\big(W+\gamma(t)\big)\Biggl)\cap C $$ and thus we conclude that the immage of $\phi$ is open in $C$ because the translations are a homeomorphism and thus $W+\gamma(t)$ is open for each $t\in I$. Now if $\overset{°}M$ and $\partial M$ are the sets of the interior and boundary points of $M$ then we observe that $C$ is union of the sets $$ \bigcup_{t\in\text{int}\, I}\big(\overset{°}M+\gamma(t)\big)\,\,\,\text{and}\,\,\,\bigcup_{t\in\text{bd}\, I}\big(\overset{°}M+\gamma(t)\big)\,\,\,\text{and}\,\,\,\bigcup_{t\in I}\big(\partial M+\gamma(t)\big) $$ so that we analyse separately the case where $\xi$ is an element of the first set and the case where $\xi$ is an element of the second or either of the third: in particular this means to analyse separately the case where the set $ U $ is open in $ \Bbb R^{n-1} $ and $ t $ is an element of $ \text{int} \, I $ and the case where this is not and so just this is what we will do to follows -clearly this can be done independentely from the definition of the three mentioned sets nevertheless we decided to define them because we thought it makes more clear the following argumentetions, that's all. In particular in the example posted above these sets are respectively the invisible part, the red part, the green and balck parts. So first of all we observe that if $\xi$ is an element of the first set then $\alpha$ is a coordinate patch of $M$ defined in an open set $U$ of $\Bbb R^{n-1}$ and so the map $\phi$ defined above is a diffeomorphism in a neighborhood at any point of $U\times\text{int}\,I$ where is contained $\phi^{-1}(\xi)$, because if the unit tangent vector of $\gamma$ not lies to the tangent space at any point of $M$ then the derivative of $\phi$ is an isomorphism and so the statement follows directely from the inverse function theorem. So we conclude that the set $$ \bigcup_{t\,\in\,\text{int}\,I}\big(\overset{°}M+\gamma(t)\big) $$ is a $n$-manifold without boundary. In particular in this way we proved that the invisible part of the linked example is a manifold without boundary. Now if $\xi$ is a not an element of the first set then the previous argumentations hold only with some efforts that we show to follow. So the functions $\alpha$ and $\gamma$ can be extended to two $C^r$-functions $\beta$ and $\psi$ defined in a open neighborhood of $U$ and $I$ respectively so that the function $\phi$ can be extended to a function $\varphi:=\beta+\psi$ defined in a open neighborhood of $U\times I$ and in particular at any point $(x,t)$ of $U\times I$ this function has not singular derivative so that by the inverse function theorem there exist a (rectangular) open neighborhood $W_x\times W_t$ where $\varphi$ is a diffeomorphism. Now the set $\varphi[W_x\times W_t]$ is open in $\Bbb R^n$ and it is not disjoint from $C$ -indeed $W_x\times W_t$ is not disjoint from $U\times I$ and $\varphi$ is compatible with $\phi$ in $U\times I$ and the immage of $\phi$ is contained in $C$- so that by the continuity of $\phi$ the set $$ \phi^{-1}[\varphi[W_x\times W_t]] $$ is (not empty and) open in $U\times I$ and contains $W_x\times W_t\cap U\times I$ where $\phi$ is a diffeomorphism. So if we prove that the immage of $W_x\times W_t\cap U\times I$ through $\phi$ is open in $C$ then we conclude that the restriction of $\phi$ to this set is a coordinate patch defined in a open set of $\Bbb R^{n-1}\times[0,+\infty)$ or in a open set of $\Bbb R^{n-2}\times[0,+\infty)^2$ if $U$ is open in $\Bbb R^{n-1}$ and $t$ is not an element of $\text{int}\, I$ or if $U$ is not open in $\Bbb R^{n-1}$ and $t$ is an element of $\text{int}\, I$ or either if $U$ is not open in $\Bbb R^{n-1}$ and $t$ is not an element of $\text{int}\, I$ respectively. So how do this? Could someone help me, please?

To follows some observations that I tried to use: naturally you are not constrained to read it if you do not desidre.

OBSERVATION

If the function $\phi$ was injective in $U\times I$ the statement follows immediately because in particular the function $\varphi$ would be injective in $W_x\times W_t\cup U\times I$ so that $$ \phi[W_x\times W_t\cap U\times I]=\varphi[W_x\times W_t\cap U\times I]=\varphi[W_x\times W_t]\cap\varphi[U\times I]=\\ \varphi[W_x\times W_t]\cap\phi[U\times I] $$ having remembered that $\varphi$ and $\phi$ are compatible in $U\times I$. So in particular we observe that the injectivity of $\phi$ follows immediately if the set $M+\gamma(t_0)$ and $M+\gamma(t_1)$ was disjoint for any $t_0,t_1\in I$ such that $t_0\neq t_1$ and in particular I tried to prove this using the injectivity of $\gamma$ that above I did not use. Moreover since $\alpha$ is a homeomorphism and since $W_x$ is open in $\Bbb R^{n-1}$ then $\alpha[W_x\cap U]$ is open in $M$ and so exist a open set $W$ of $\Bbb R^n$ whose intersection with $M$ is $\alpha[W_x\cap U]$ and thus implementing the argumentations used above it follows that $$ \phi[W_x\times W_t\cap U\times I]=...=\Biggl[\bigcup_{t\in W_t\cap I}\big(W+\gamma(t)\big)\Biggl]\cap\Biggl[\bigcup_{t\in W_t\cap I}\big(M+\gamma(t)\big)\Biggl] $$ so that if the set $\Biggl[\bigcup_{t\in W_t\cap I}\big(M+\gamma(t)\big)\Biggl]$ and $\Biggl[\bigcup_{t\in I\setminus W_t}\big(M+\gamma(t)\big)\Biggl]$ was disjoint then $\phi[W_x\times W_t\cap U\times I]$ was open in $C$ and this surely happens if the set $M+\gamma(t_0)$ and $M+\gamma(t_1)$ was disjoint for any $t_0,t_1\in I$ such that $t_0\neq t_1$.

Answer 1

The cylindroid C need not be a manifold with corners. Here's a sketch of a counterexample (different from the incorrect one I posted earlier). Forgive my crude drawings.

Begin with a surface in $\mathbb R^3$ that's diffeomorphic to a disk. Looking down on it from the positive $z$-axis, its projection on the $xy$-plane looks like this: But in 3-d, it actually lies on the surface of a helicoid, so as you walk counterclockwise around the surface, you gradually rise one unit in the $z$-direction. The darkened point on the positive $x$-axis actually represents two points on the surface, with one of them $1$ unit above the other.

Now let $\gamma:[0,1]\to \mathbb R^3$ be the curve $\gamma(t) = (0,0,t)$. The cylindroid $C$ is thus obtained by taking this helicoidal surface and translating it directly upward one unit. The resulting solid figure looks roughly like this: The red dot is the point where the original surface meets its translated version. There is no neighborhood of the red dot in $C$ that is homeomorphic to an open subset of $\mathbb R^3$ or of $H^3_k$ for any $k$.

ADDED: Assume for contradiction that $C$ is a manifold with corners. Since some points of $C$ have neighborhoods homeomorphic to open balls in $\mathbb R^3$, it must be $3$-dimensional by invariance of dimension. Our assumption implies that there is a (relative) neighborhood $U$ of the red point in $C$ and a homeomorphism $\varphi\colon U\to \widehat U$, where $\widehat U$ is an open subset of $\mathbb R^3$ or of $H^3_k$ for some $k$. By shrinking $U$ and $\widehat U$ if necessary, we can assume both are connected. Shrinking further, we can assume that $U$ is contained in the ball of radius $1/8$, say, around the red point.

Now let $q = \varphi(\text{red point})$. Then $\widehat U\smallsetminus\{q\}$ is connected, but $U\smallsetminus \{\text{red point}\}$ is disconnected. Since homeomorphisms preserve connectivity, this is a contradiction.