2

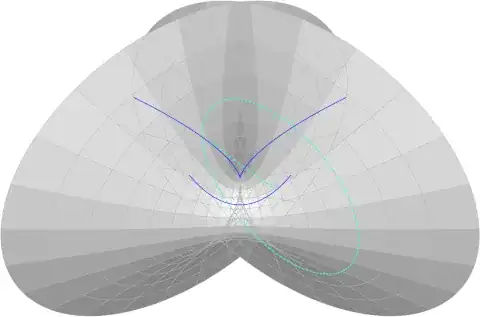
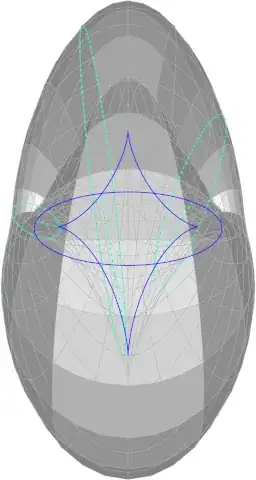
For the last few years, I have tried a couple times to solve this problem that I came up with. Even though this may seem like a nonsensical idea, there is still a seed of wonder embedded into it.

This problem is the one about having one “functional or relational” axis in which the other function goes around it. Let this operator be called $\operatorname{Rev}(f,g)$ where g is the axis function and f is the function which “Revolves” around it hence the name “Rev”. This can be thought of as a circle.

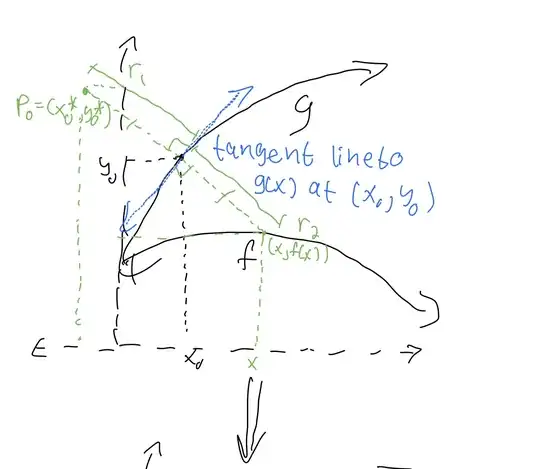
Let’s think about splitting each “revolution” of a point around another point as one revolution. I believe one great way to see this would be to choose a point $(x_i,y_i)$ and draw the tangent line at that point to the axis.

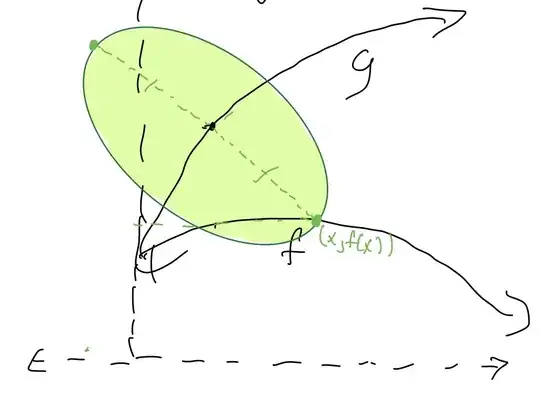
Afterwards, the normal line to the point would be drawn until it intersects the other relation. The length of this line would be r and so would the line in the other direction extending to the other side of the tangent line. I apologize if my diagrams are a bit unprofessional: enter image description here

Following from the rest of the diagram, the diameter can be used to draw a circle, or ellipse from this point of view: enter image description here

Completing this process for every point on the relation axis would get us the unfilled and hollow surface of $\operatorname{Rev}(f,g)$.

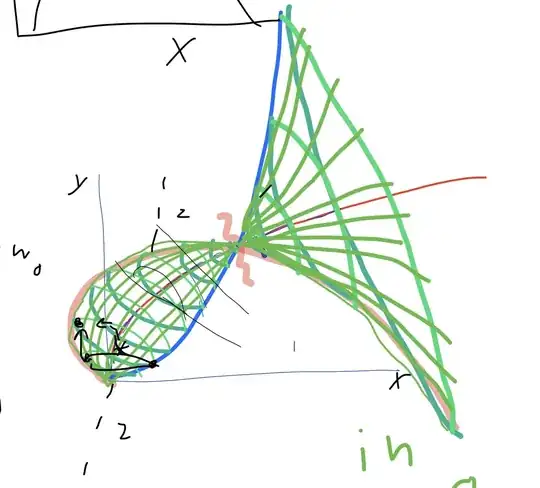
Here is what the revolution of $\sqrt x and x^2$ would look like or $\operatorname{rev}(x^2,\sqrt x)$: enter image description here

I have been successful with the slice of the function with the z=0 plane and $\operatorname{Rev}(3x,2x)$ which I solved this way:

First we need to find the general equation for (x,f(x)) in the diagram which has x=a(t) as a parametrization , and so equals (a,f(a)). $\operatorname{a}(t)$ is simply a line with point-slope form of f(x)=-$\frac{1}{g’(t)}(x-t)+g(t)$=$\frac{t-x}{g’(t)}+g(t)$⇔x=a(t). One must solve the system to find the x-function.

This relation can be then put into the form of the normal line vector of $\langle (x_0-t,g(x_0)-f(a(t))\rangle$ because of the start and endpoints in the graph.

By solving both of these, we get $\operatorname{Rev}(3x,2x)$ in the plane z=0 to be the parametric line $\overrightarrow{A}(t)=(x=\frac{3}{10}t,y=\frac 85 t)$ or 2x. Solving the parametric equation for the answer gets y=$\frac{16}{3} x$.

Using the Join function gets us our final answer for the first part as $\operatorname{Join}(\frac{16}{3}x,\frac{8}{3}x)$=$\frac{11}{3}x\pm\frac 53 x$=($11\pm5)\frac{x}{3}$.

Try graphing all three line functions on desmos!

https://www.desmos.com/calculator/rw8pcv9yzo

Unfortunately, the rest of the examples with negative slopes and non-linear relations have left me wondering what went wrong.

This means that main question is what would be the formula for writing the surface of revolution for any two relations? At the very least, a parametric equation should do the job. I know Dr.Piam did a video about a revolution around y=x using linear algebra: https://m.youtube.com/watch?v=ZzYDmbq_Oqg

However, this technique described above should be good enough.

So please, I am looking for people to really answer this question, if they want and if they can, not just a small hint. If you have a final answer to this problem, please write it down below! This should be easy enough to do. Simply follow the process and write the formulas out.

Also try answering my previous question which can easily be done with software! It is for anyone interested in trigonometry or geometry:

Exact Expressions of Sine and cosine of a*$\frac{\pi}{n}$ with $n=11,13,19,23$ (and others)

Here are some useful links: https://en.m.wikipedia.org/wiki/Surface_of_revolution

Volume of a solid from rotating a function around a non-linear axis of rotation

https://www.reddit.com/r/askmath/comments/61in1g/solid_of_revolution_around_a_nonlinear_axis/

Тyma Gaidash
  • 12,081
  • 1
    Related, though not identical if I understand your description. (The difference is, you take the radius to be given by where the normal line to $g$ hits $f$; in the linked post, the value of $f$ itself would be used as radius.) – Andrew D. Hwang Apr 03 '21 at 14:42
  • The problem with getting a parametrization of the type you request (and the impossibility of doing so in closed form using only $f$ and $g$) is the difficulty of calculating where a general line crosses a curve. – Andrew D. Hwang Apr 18 '21 at 22:38
  • @AndrewD.Hwang You could define the function, for example a(t), as the function such that a line crosses a curve. You could also use inverse functions even though restrictions may come with those. – Тyma Gaidash Apr 19 '21 at 12:13
  • IIRC, a line can intersect a curve in multiple points, but if an answer in terms of your $a(t)$ is acceptable, that's easy to write down. – Andrew D. Hwang Apr 19 '21 at 15:54

1 Answers1

1

In the interest of computational flexibility, let's work parametrically: We're given a continuous plane curve $f(s) = \bigl(x(s), y(s)\bigr)$ and a regular (continuously-differentiable, non-zero velocity) plane curve $g(t) = \bigl(u(t), v(t)\bigr)$, and want to parametrize the surface obtained by "revolving $f$ about $g$".

Tangent and unit normal vectors to $g$ at $g(t)$ are $$ g'(t) = \bigl(u'(t), v'(t)\bigr),\qquad n(t) = \frac{\bigl(-v'(t), u'(t)\bigr)}{\sqrt{u'(t)^{2} + v'(t)^{2}}}. $$ Let $a(t)$ denote the real number of smallest absolute value for which $g(t) + a(t)n(t) = f(s)$ lies on $f$. (As noted in the comments, finding $a(t)$ is generally a matter of numerical approximation, the point of intersection of a curve and a line.) The desired surface is parametrized by \begin{align*} X(t, \theta) &= g(t) + a(t)\bigl(\cos\theta\, n(t) + \sin\theta (0, 0, 1)\bigr) \\ &= \biggl[u(t) - \frac{a(t) v'(t) \cos\theta}{\sqrt{u'(t)^{2} + v'(t)^{2}}}, v(t) + \frac{a(t) u'(t) \cos\theta}{\sqrt{u'(t)^{2} + v'(t)^{2}}}, \frac{a(t) \sin\theta}{\sqrt{u'(t)^{2} + v'(t)^{2}}}\biggr]. \end{align*}

In the examples shown, $f$ is taken to be the evolute of $g$, so that $s = t$ and $a(t) = \|g(t) - f(t)\|$.

$g(t) = (t, t^{2})$ the standard parabola, $f(t) = (-4t^{3}, \frac{1}{2} + 3t^{2})$ a cubic cusp:

Revolving a cusp about a parabola

$g(t) = (a\cos t, b\sin t)$ an ellipse, $f(t) = \frac{a^{2} - b^{2}}{ab}(b\cos^{3}t, -a\sin^{3} t)$ an astroid:

Revolving an astroid about an ellipse

Andrew D. Hwang
  • 78,195
  • If $f(s)=(s,s^2),g(t)=(t,\sqrt t)$, with $f(s)$ and $g(t)$ both in the $xy$ plane as illustrated in the question, then the equation for $a(t)$ is $\left(t-a \frac{\frac1{2\sqrt t}}{\sqrt{\left(\frac1{2\sqrt t}\right)^2+1^2}} ,\sqrt t+a \frac1{\sqrt{\left(\frac1{2\sqrt t}\right)^2+1^2}}\right)=(s,s^2)$. Perhaps $\sqrt t+a,n(t)=s^2$ would work. Either way, how would you find $a(t)$? – Тyma Gaidash Oct 09 '23 at 18:54
  • 1
    If I recall the meaning of the notation, the issue is to find, for a given parameter value $t$ and with $n(t)$ denoting a unit normal at $g(t)$, the smallest number $a(t)$ such that $g(t) \pm a(t)n(t)$ lies on the image of $f$, i.e., is of the form $f(s)$ for some $s$. <> Even if your main interest is parabolas, that may be best addressed by asking a separate question...? The answer looks likely to involve either the cubic or quartic formulas, or numerical methods. – Andrew D. Hwang Oct 10 '23 at 01:33