1

In Calculus class, we are all taught how to find the volume of a solid of rotation around any line of the form $y=a$ or $x=b$. Then in linear algebra, we are taught how to find the volume of a solid of rotation around a line of the form $y=mx$ by using the rotation matrix, $\begin{bmatrix} \cos (x) & -\sin (x)\\ \sin (x) & \cos (x) \end{bmatrix}$. But is it possible to find the volume of a solid that is rotated around a non-linear axis of rotation? For example, let's say that we are rotating the function $f(x) = -x^{2} + \frac{2}{\pi } x + \frac{\pi ^{2}}{4}$ around axis of rotation $g(x) = \sin (x)$. Notice that f(x) only intersects with g(x) at two points: $\left ( -\frac{\pi }{2},-1 \right )$ and $\left ( \frac{\pi }{2},1 \right )$. So we are only rotating f(x) around g(x) between those two intersections. I provide an image just to help with visualization. The red function is the axis of rotation, the green function is the function which we are rotating, and the black lines represent the bounds of rotation. My question is then, what is the volume of that solid of rotation? The only thing I found related to this was from this question,Solids of Revolution around other functions. , but the question was still left unanswered and this question is just a slight variant of that one.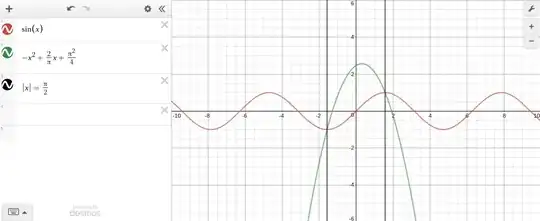

edit: Based on the comments, I tried to come up with a way to define a rotation around a non-linear axis, and this is what I have come up with. Let us cover the non-linear axis of rotation with an abundance of tangent lines of length $\Delta L $. We can rotate a function around each of those lines of length $\Delta L $. The solid of rotation would then be the solid that comes from combining all the solids generated from rotating around each of those tangent lines of length $\Delta L $ as $\Delta L \rightarrow 0$ Would this make sense as a definition of rotating around a non-linear axis?

2nd edit: In the comments, you can find a better definition to define this concept.

Eliot
  • 114
  • How can you define this rotation? An axis of rotation must be a straight line. – Peter Foreman Apr 17 '19 at 21:23
  • I am not sure how to define the rotation. I was thinking maybe there is some way to extend the definition to "rotate" around something non-linear, but I am not sure if such a way exists. – Eliot Apr 17 '19 at 21:28
  • 1
    Perhaps you should ask or think about what a rotation about a nonlinear curve might be, before worrying about volumes. Perhaps slice the space around the curve into planes orthogonal to it, and specify rotations in each plane. This will not work globally as those planes will start crossing each other far enough from the curve. – Conifold Apr 17 '19 at 21:36
  • @Conifold I edited my comment to give what I think could be a definition of rotating around a non-linear axis. – Eliot Apr 17 '19 at 21:51
  • "Solid that comes from combining all the solids" does not make much sense. You'll get infinitely many solids produced by rotating around different tangent lines, and how they are combined into one is not clear. "As $\Delta L \rightarrow 0$" even less so. Your $\Delta L$ is fixed as the distance from the curve to the axis. What you can do is draw perpendicular planes to the red curve at each point, and draw circles of radius $\Delta L$ in each plane ($\Delta L$ is the distance to the green curve in the plane). For close enough curves this gives a kind of "solid of revolution". – Conifold Apr 17 '19 at 22:10
  • @Conifold yeah I see where you're getting and I was just thinking of that way. However, I think that would be too tedious to work it out for the volume. I think I'm satisfied enough with this though. – Eliot Apr 17 '19 at 22:21
  • 1
    It's actually quite easy, you just integrate areas of circles with known radii along the red curve. Finding the radii explicitly might be somewhat challenging. – Conifold Apr 17 '19 at 22:27
  • @Conifold yeah that is what I meant about it being tedious. – Eliot Apr 17 '19 at 22:29
  • 2
    Perhaps. But drawing normals and finding distances from points to curves is a classical geometric problem with a long history (goes back to Apollonius), and rich theory. For parabolas, see The Normals to a Parabola. It is good that you are thinking beyond the four corners of textbooks' definitions. Do not be deterred by the seeming intractability of where it leads. One thing leads to another, and it gets fascinating. – Conifold Apr 17 '19 at 22:36

1 Answers1

2

Let $$\gamma:\quad s\mapsto{\bf r}(s)=\bigl(x(s),y(s),z(s)\bigr)$$ be a "curved" space curve, parametrized by arc length $s$. Along $\gamma$ we have the Frenet frame, attached at the moving point ${\bf r}(s)$: $$\eqalign{{\bf t}(s)&:=\dot{\bf r}(s)\cr {\bf n}(s)&:={\dot{\bf t}(s)\over|\dot{\bf t}(s)|}\cr {\bf b}(s)&:={\bf t}(s)\times {\bf n}(s)\cr}$$ Here ${\bf t}$ is the unit tangent vector, and it is assumed that $\dot{\bf t}(s)\ne{\bf 0}$. The vectors ${\bf n}(s)$ and ${\bf b}(s)$ then are an orthonormal basis of the normal plane to $\gamma$ at ${\bf r}(s)$.

We now assume that an additional radius function $s\mapsto\rho(s)>0$ is given. We then can create a tube $S$ along $\gamma$, of varying thickness $2\rho(s)$, by putting $$S:\quad (s,\phi)\mapsto {\bf p}(s):={\bf r}(s)+\rho(s)\bigl(\cos\phi\>{\bf n}(s)+\sin\phi\>{\bf b}(s)\bigr)\ .$$ This $S$ may have selfintersections when $\rho(s)$ is too large in relation to the curvature $\kappa(s)$ along $\gamma$.

Christian Blatter
  • 226,825