Extending $\sum_{n=0}^\infty s^{n^2}$ beyond its natural boundary

Question

Let $\mathbb{D} = \{s \in \mathbb{C} : |s| < 1\}$. Let $f : \mathbb{D} \rightarrow \mathbb{C}$ where $$ f(s) = \sum_{n=0}^\infty s^{n^2} $$ $f$ is analytic on $\mathbb{D}$. This is what it looks like: $\partial \mathbb{D}$ is a natural boundary, so ordinary analytic continuation cannot extend $f$ beyond $\mathbb{D}$. However, there might be another way to extend $f$ beyond $\mathbb{D}$ that is both aesthetically natural and yields a unique result. For example, see generalized analytic continuation and Continuation of functions beyond natural boundaries.

Let $$ \Delta = \left\{\exp \left( 2\pi i \frac{2n + 1}{4m + 2} \right) : m, n \in \mathbb{Z}\right\} \subseteq \partial \mathbb{D} $$ Note that $\Delta$ is dense. It seems that \begin{align} \lim_{\substack{s \rightarrow \omega \\ s \in \mathbb{D}}} f(s) &= \frac{1}{2} \\ \lim_{r \uparrow 1} \partial_r f(r \omega) &= 0 \end{align} for all $\omega \in \Delta$. I have 2 questions:

1. Are there other $\omega \in \partial \mathbb{D} \setminus \Delta$ for which the above limits exist?
2. Is there an analytic (or meromorphic) $g : \mathbb{C} \setminus \overline{\mathbb{D}} \rightarrow \mathbb{C}$ such that \begin{align} \lim_{\substack{s \rightarrow \omega \\ s \in \mathbb{C} \setminus \overline{\mathbb{D}}}} g(s) &= \lim_{\substack{s \rightarrow \omega \\ s \in \mathbb{D}}} f(s) \\ \lim_{r \downarrow 1} \partial_r g(r \omega) &= \lim_{r \uparrow 1} \partial_r f(r \omega) \end{align} for all $\omega \in \partial \mathbb{D}$ such that both sides are defined, and such that the LHS is undefined iff the RHS is undefined? That is, such that $g$ “matches” $f$ along $\partial \mathbb{D}$, in some sense? If so, is it unique? If not, are there additional conditions, perhaps some analogue of the identity theorem, that can give us a unique extension?

Answer 1

Well, I'm a month late, but I wanted to go further with something Daniele mentioned in the comments. I've been considering something similar for a while, and I think the Laurent strategy Daniele mentioned is close to what I view as the correct answer is.

First, let's look at how something similar to the Laurent series can be used to analytically continue some of the more commonly seen functions. For instance, if we wished to continue $$f(x) = \sum_{n=0}^\infty nx^n$$ We could simply use the fact that $\sum_{n=0}^\infty nx^n = \sum_{n=0}^\infty n^{-(-1)}x^n = Li_{-1}(x)$, and Li is defined for all x values. We can extend this to finite sums of powers of n, so we could see that $$f(x) = \sum_{n=1}^\infty (n+3n^2-n^3)x^n = Li_{-1}(x) + 3Li_{-2}(x)-Li_{-3}(x)$$ But, why have I introduced logarithmic integrals in relatively simple problems? Logorithmic integrals happen to have an incredibly fortunate method for continuation, which his that, for $|x|>1$, $$Li_{-k}(x)=(-1)^{1+k}\sum_{n=1}^\infty n^kx^{-n}$$ This tells us that for the previous problems, we could have done $$\sum_{n=1}^\infty (n+3n^2-n^3)x^n = \sum_{n=1}^\infty nx^n+3\sum_{n=1}^\infty n^2x^n-\sum_{n=1}^\infty n^3x^n$$ can be continued to $$\sum_{n=1}^\infty nx^{-n}+3\sum_{n=1}^\infty n^2x^{-n}+\sum_{n=1}^\infty n^3x^{-n}=\sum_{n=1}^{\infty}\left(n-3n^{2}-n^{3}\right)x^{-n}$$ when |x|>1, and when |x|<1 we can use the regular sum. This fact allows us to gain a power and easy way to extend functions of the form $\sum_{n=1}^\infty f(n)x^n$ which have power series for f(n). $$\sum_{n=1}^\infty f(n)x^n = \sum_{n=1}^\infty \sum_{k=0}^\infty x^nb_kn^k $$ if one allows blindly interchanging the summations $$\sum_{k=1}^\infty b_k\sum_{n=0}^\infty x^nn^k = \sum_{k=1}^\infty b_k(-1)^{1+k}\sum_{n=0}^\infty x^{-n}n^k = -f(0)+\sum_{n=1}^\infty x^{-n}\sum_{k=1}^\infty b_k(-n)^k = -f(0)+\sum_{n=1}^\infty x^{-n}f(-n)$$ Then this method gives us a powerful method to continue functions which have a 'natural' power series, but struggles with the fact that $f(n)$ doesn't carry enough information to uniquely define a power series.

In particular, for this question, one possible valid definition for $f(n)$ is $$f(x) = \frac{\sin\left(\pi\left(x\right)\right)}{\pi\left(x\right)}+\sum_{k=1}^{\infty}\left(\frac{\sin\left(\pi\left(x-k^{2}\right)\right)}{\pi\left(x-k^{2}\right)}+\frac{\sin\left(\pi\left(x+k^{2}\right)\right)}{\pi\left(x+k^{2}\right)}\right)$$ which corresponds to what Daniele got, since $f(n) = f(-n)$, and so this is one reason why Daniele's method happened to get something that works well.

I think there is at least a few reasons to prefer something like this for continuing this gap series. For one, it sort of generalizes square numbers. Since $$\> 2 \quad 2 \quad 2 \quad 2 \quad 2 $$ $$\>\>\>\> \text{-}5 \quad \text{-}3 \quad \text{-}1 \quad 1 \quad 3 \quad 5 \quad$$ $$\text{ }9 \quad \text{ }4 \quad \text{ }1 \quad \text{ }0 \quad \text{ }1 \quad \text{ }4 \quad 9$$ seems to suggest that an extension of squared numbers should be even, whereas doing the same process of $n^3$ gives negatives on one side, and positive on the other, which suggests it should be odd. Indeed, choosing $f(n)$ is even when $n^k$ is even, and $f(n)$ is odd when $n^k$ is even produces continuous extensions, while doing it the opposite way does not.

Further, one can show that the two functions, $$\sum_{n=0}^\infty x^{(n^2)} \text{ and } \sum_{n=0}^\infty x^{(-n^2)}$$ have derivatives that are all zero and agree at -1 by applying some regularizations to allow the functions to converge all the way up -1. The functions also just seem to mesh together in a natural way: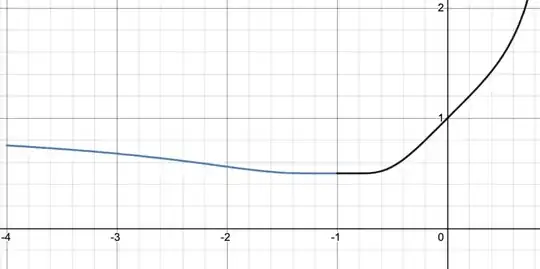

I think this is only a first step, though, since the uniqueness problem is not addressed in any rigorous fashion--but I think they're some good reasons to think this is a good option for being the correct continuation. Let me know if you guys have any ideas on this.