How far can the convergence of Taylor series be extended?

Question

Taylor series can diverge and have only a limited radius of convergence, but it seems that often this divergence is more a result of summation being too narrow rather than the series actually diverging.

For instance, take $$\frac{1}{1-x} = \sum_{n=0}^\infty x^n$$ at $x=-1$. This series is considered to diverge, but smoothing the sum gives $\sum_{n=0}^\infty (-1)^n = \frac{1}{2}$, which agrees with $\frac{1}{1-(-1)}$. Similarly, $$\sum_{n=0}^\infty nx^n = x\frac{d}{dx}\frac{1}{1-x} = \frac{x}{(1-x)^2}$$ normally diverges at $x=-1$, but smoothing the sums gives $-\frac{1}{4}$ which agrees with the function. This process continues to hold for any number of taking the derivative than multiplying by x.

One can extend series of these types even further. Taking $$\frac{1}{1+x} =\sum_{n=0}^\infty (-x)^n = \sum_{n=0}^\infty (-1)^ne^{\ln(x)n} = $$ $$\sum_{n=0}^\infty (-1)^n\sum_{m=0}^\infty \frac{\left(\ln(x)n\right)^m}{m!} = \sum_{m=0}^\infty \sum_{n=0}^\infty (-1)^n\frac{\left(\ln(x)n\right)^m}{m!} = $$ $$\sum_{m=0}^\infty\frac{\ln(x)^m}{m!} \sum_{n=0}^\infty (-1)^n n^m = 1 -\sum_{m=0}^\infty\frac{\ln(x)^m}{m!} \eta(-m)$$

This sum converges for all values of $x>0$ and converges to $\frac{1}{1+x}$

In general, one can transform any sum of the form $$ \sum_{k=1}^\infty a_k x^k = -\sum_{k=0}^\infty \left(\sum_{n=-\infty}^\infty b_k x^k\right) (-1)^n x^n =$$ $$ -\sum_{k=0}^\infty b_k \sum_{m=0}^\infty\frac{\ln(x)^m}{m!}\eta(-(n+k)) $$

In general, how much is it possible to extend the range of convergence, simply by overloading the summation operation (here I assign values based on using the eta functions, but I can imagine using something like Abel regularization or other regularization)? Are there any interesting results that come from extending the range of convergence to the Taylor series?

One theory I had was that the Taylor series should converge for any alternating series which has a monotonic $|a_k|$. Is this true? Are there any series that are impossible to increase their radius of convergence by changing the sum operation? In short, my goal is to find a way of overloading the sum operation that widens the radius of convergence of the Taylor series as far as possible while still agreeing with the function.

Edit: I wanted to add that it might be useful in looking at this question to know that $$ \sum_{m=0}^\infty\frac{\ln(x)^m}{m!}\eta(-(m-w))= -Li_w(-x) $$ where $Li_w(-x)$ is the wth logarithmic integral. So the sum method I provided transforms a sum to an (in)finite series of logarithmic integrals.

---

This is sort of tangential, but I was reflecting a bit more on this problem, and it seems to be that a Taylor series has enough information to be able to extend a sum until the next real singularity. For instance, if I graph a function in the complex plane, then the radius of convergence is the distance to the nearest singularity. In this image, I have a few different singularities (shown as dots). 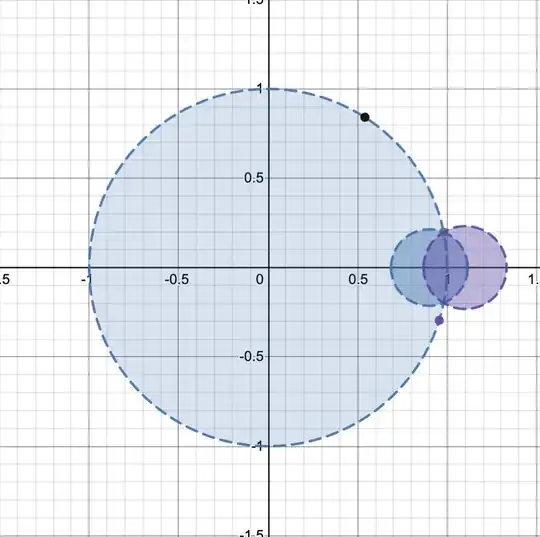But, since the original Taylor series (call it $T_1(x)$, its shown as the large blue circle in the image) will exactly match the function within this disk, its possible to get another Taylor series (call it $T_2(x)$, its shown as the small blue circle) centered around another point while only relying on derivatives of $T_1(x)$. From $T_2(x)$, its possible to get $T_3(x)$ (the purple circle), which extends the area of convergence even further. I think this shows that the information contained by the Taylor series is enough to end all the way to a singularity on the real line, rather than being limited by the distance to a singularity in the complex plane. The only time this wouldn't work is if the set of points on the boundary circle where the function divergences is infinite and dense enough to not allow any circles to 'squeeze though' using the previous method. So in theory, it seems like any Taylor series which has a non-zero radius of convergence and a non-dense set of singularities uniquely determines a function that can be defined on the entire complex plane (minus singularities).

Edit 2: This is what I have so far for iterating the Taylor series. If the Taylor series for $f(x)$ is $$T_1(x)=\sum_{n=0}^\infty \frac{f^{(n)}}{n!}\left(0\right) x^n$$ and the radius of convergence is R, then we can center $T_2(x)$ around $x=\frac{9}{10}R$, since that is within the area of convergence. We get that $$T_2(x) = \sum_{n=0}^\infty \frac{T_1^{(n)}}{n!}\left(\frac{9}{10}R\right) x^n = $$ $$T_2(x) = \sum_{n=0}^\infty \left(\frac{\sum_{k=n}^\infty \frac{f^{(k)}\left(0\right)}{k!} \frac{k!}{(k-n)!} \left(\frac{9}{10}R\right)^{k-n}}{n!}\right) x^n = \sum_{n=0}^\infty \left(\sum_{k=n}^\infty f^{(k)}\left(0\right) \frac{1}{(k-n)!n!} \left(\frac{9}{10}R\right)^{k-n}\right) x^n $$ and in general centered around $x_{center}$ $$T_{w+1}(x) = \sum_{n=0}^\infty \frac{T_w^{(n)}\left(x_{center}\right)}{n!} x^n$$ I tested this out for ln(x), and it seemed to work well, but I suppose it could fail if taking the derivative of $T_w(x)$ too many times causes $T_w(x)$ to no longer match $f(x)$ closely.

I tested out this method of extending a function with Desmos, here is the link if you would like to test it out: https://www.desmos.com/calculator/fwvuasolla

Edit 3: I looked in analytic continuation some, and it looks like the method I was thinking of that extends the range of convergence using the old coefficients to get new ones is already a known method, though it uses Cauchy's differentiation formula so it is able to avoid some of the convergence problems that I was worried about before that comes from repeated differentiation. So, it appears there should exist some way to overload the sum operation that achieves this same continuation. I suppose there's the trivial option of defining summation as the thing which returns the same values as continuation would return, but that's a very unsatisfying solution. It would be interesting to see if it's possible to create a natural generalization of summation that agrees with this method of continuation.

Edit 4: I think I may have found a start for how to extend the convergence of all Taylor series which can be extended. Based on my above argument of recursively applying the Taylor series, one algorithm could go as follow:

1. Get the Taylor series at the starting point (call it $x_0$)
2. Use this Taylor series to get all the points between $[x_0,x_0+dt]$
3. Recenter the Taylor series at $x_0 + dt$ to updating the derivatives
4. Repeat from 1 to continue expanding the convergence

So long as dt is smaller than the distance of the nearest singularity is to the real line, all Taylor series will converge. Now, this method isn't all that useful itself, since it requires many recursive steps, but it sets the stage for what I think is a natural way to extend summation to work for analytic continuation.

Instead of thinking of the values of the derivative as values to be summed together as a polynomial, instead view the set of derivatives at a point as seed values for applying Euler's Method. My motivation for this is that as $dt$ becomes very small, Euler method should become a successively better and better approximation of the above algorithm. When dt is sufficiently small, the values of the Euler method around $x_0$ should uniformly converge to the values that the Taylor series would give. It seems to me that this should also hold for the derivatives of the Taylor series. My main concern with this method is that each step introduces a small error and that eventually, this error would become impossible to contain, but I'm not sure how to do prove or disprove this.

Based on this, could one view the Taylor series as instead providing a differential equation with infinite initial conditions? Do differential equations say anything about the uniqueness of the existence of equations of this type? Does the Euler method actually work to extend the radius of convergence of a power series?

I've attached some code to be able to run the Euler method on different functions. I've been able to extend the convergence of a number of functions, but it is quite hard to extend it anywhere about 2~3 times further than the regular convergence range since the size of the terms grow with a factorial function, so it takes a very long time to run past that range. In the following code, I'm extending the function with the seed $a_n = n!$, which corresponds to $\frac{1}{1-x}$.

import matplotlib.pyplot as plt
import math
from decimal import Decimal
from decimal import *
getcontext().prec = 1000 #need LOTS of precision to extend the range. Even 1000 accurate places causes a problem with large factorials
def iterate(L, m):
    R = []
    for i in range(len(L)-1):
        R.append(L[i] + m*L[i+1])
    R.append(L[len(L)-1])
    return R
def createL(S):
    L = []
    for i in range(S):
        L.append(Decimal(math.factorial(i)) )
    return L
def createCorrectDeriv(S,x):
    L = []
    for i in range(S):
    L.append( pow(Decimal(1-x),-1-i)* math.factorial(i))

return L


def runEuler():
DT = -.002
dt = Decimal(DT)
W= int(-3/DT) 
print(W)
print("range converge should be: "+ str(abs(DT* W) ))
print("Size list: " + str(W))
L = createL(int(W ) )
L_val = []
Y_val = []
Z_val = []
X_val = []

for i in range( W ):




    L_val.append(L[0])

    L = iterate(L,Decimal(dt) )



    X_val.append(-dt*i)
    Y_val.append(1.0/(1-(DT*(i)) ))


plt.plot(X_val, L_val)
plt.plot(X_val, Y_val)
plt.show()







runEuler()

Final Edit: I think I figured it out! The result is (for analytic f(x)) that $$f(x) = \lim_{dt \to 0}\sum_{n=0}^\frac{x}{dt} \frac{(dt)^n}{n!} f^{(n)}(0) \prod_{k=0}^{n-1} \left(\frac{x}{dt}-k\right)$$ For $f(x) = \frac{1}{1-x}$ this becomes $$\lim_{dt \to 0} e^{\frac{1}{dt}}dt^{-\frac{x}{dt}}\int_{\frac{1}{dt}}^{\infty}w^{\left(\frac{\left(dt-x\right)}{dt}-1\right)}e^{-w}dw$$ which does indeed converge to $\frac{1}{1+x}$ for $(-1,\infty)$. Thanks for everyone's help in getting here! I'm going to work next on seeing if allowing dt to be a function of the iterations allows one to extend this method to get analytic continuations of functions which have boundaries that are dense but not 100% dense, since my thought is that maybe after an infinite number of steps its possible to squeeze through the 'openings' in the dense set.

Answer 1

Introduction

There exists powerful methods that allow you to do these sorts of computations in an efficient way. These methods are often used in theoretical physics, but usually not in a mathematically rigorous way. We then don't attempt to extend the radius of convergence in a step-by-step way as described in the problem, because typically we have to deal with a asymptotic expansion that has zero radius of convergence. In some cases the problem is to find the limit of the expansion parameter tending to infinity or even find the first few terms of the expansion around infinity.

Given a function $f(x)$ defined by a series:

$$f(x) = \sum_{n=0}^{\infty} c_n x^n$$

one can consider operations on the function yielding another function $g(x)$

$$g(x) = \phi[f(x)]$$

where $\phi$ is an operator that can involve algebraic operations involving $f(x)$ and its derivatives. Methods such as Padé approximants and differential approximants fall into this category. A different class of methods use a transform on the argument of the function:

$$g(z) = f\left[\phi(z)\right]$$

These so-called conformal mappings have the advantage that they can move singularities in the complex plane and thereby make the radius of convergence larger without having to be fine-tuned to the function $f(x)$ to cancel out such singularities. What makes these methods powerful is that they can be used when only a finite number of terms the expansion are known. One then needs to choose the conformal mapping $\phi(z)$ such that $\phi(0) = 0$.

Order dependent mapping method

The question is then how to choose the mapping $\phi(z)$ when we have limited knowledge of the properties of $f(x)$. A method that works well is the so-called order dependent mapping method developed developed by Zinn-Justin. This involves using a suitably chosen conformal mapping that includes a parameter and then to choose that parameter such that the last known term of the series becomes zero. The idea here is that typically you get the best results when summing a series to the term with the least absolute value. The error when summing an asymptotic series this way is beyond all orders, and is for this reason known as the superasymptotic approximation.

The order dependent mapping method thus amounts to tuning the conformal mapping such that the superasymptotic approximation becomes the sum of all the known terms. Zinn-Justin's method uses conformal mappings of a special form and prescribes how to choose the parameter from the set of all solutions that makes the last term equal to zero. I have improved and generalized this method to more general choices for the mapping which can include more than one parameter.

To illustrate how this method works in practice, let's consider estimating $\lim_{x\to\infty}\arctan(x)$ using the series expansion of $\arctan(x)$ to order 15. So, we have:

$$f(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} - \frac{x^{11}}{11} + \frac{x^{13}}{13} - \frac{x^{15}}{15} +\mathcal{O}\left(x^{17}\right)$$

We pretend that we don't know what the next terms of the series expansion are, but we do know that $\lim_{x\to\infty} f(x)$ exists and that an expansion around infinity in positive integer powers of $x^{-1}$ exists.

The first step is to rewrite the function to get to a series with both even and odd powers: $$g(x) = \frac{f(\sqrt{x})}{\sqrt{x}} = 1 - \frac{x}{3} + \frac{x^2}{5} - \frac{x^3}{7} + \frac{x^4}{9} - \frac{x^{5}}{11} + \frac{x^{6}}{13} - \frac{x^{7}}{15} +\mathcal{O}\left(x^{8}\right)\tag{1}$$

The function $g(x)$ will then for large $x$ have an expansion on powers of $x^{-1/2}$ with the first term being a term proportional to $x^{-1/2}$. We want to find the coefficient of $x^{-1/2}$ of this expansion. We can then choose the following conformal mapping:

$$x = \phi(z) = \frac{p z}{(1-z)^2}$$

The point at infinity is then mapped to $z = 1$. If we put $z = 1-\epsilon$, then we see that $\phi(1-\epsilon)\sim \epsilon^{-2}$. Since $g(x)$ has an expansion for large $x$ in powers of $x^{-1/2}$,this becomes an expansion is positive powers of $\epsilon$ which will be consistent with what we're bound to get when re-expanding the series (1) and then substituting $z = 1-\epsilon$ in there. To extract the coefficient of $x^{-1/2}$ we need to consider the expansion of $\sqrt{p}g\left[\psi(z)\right]/(1-z)$. It follows from (1) that:

$$\frac{g\left[\psi(z)\right]}{1-z} = 1+\left(1-\frac{p}{3}\right) z+\left(\frac{p^2}{5}-p+1\right) z^2+\left(-\frac{p^3}{7}+p^2-2 p+1\right) z^3+\left(-\frac{p^3}{7}+p^2+\frac{1}{63} \left(7 p^4-54 p^3+126 p^2-84 p\right)-2 p+1\right) z^4+\left(-\frac{p^3}{7}+p^2+\frac{1}{63} \left(7 p^4-54 p^3+126 p^2-84 p\right)+\frac{1}{99} \left(-9 p^5+88 p^4-297 p^3+396 p^2-165 p\right)-2 p+1\right) z^5+\left(\frac{p^6}{13}-\frac{10 p^5}{11}+4 p^4-\frac{57 p^3}{7}+8 p^2+\frac{1}{63} \left(7 p^4-54 p^3+126 p^2-84 p\right)+\frac{1}{99} \left(-9 p^5+88 p^4-297 p^3+396 p^2-165 p\right)-4 p+1\right) z^6+\left(\frac{p^6}{13}-\frac{10 p^5}{11}+4 p^4-\frac{57 p^3}{7}+8 p^2+\frac{1}{63} \left(7 p^4-54 p^3+126 p^2-84 p\right)+\frac{1}{99} \left(-9 p^5+88 p^4-297 p^3+396 p^2-165 p\right)+\frac{1}{195} \left(-13 p^7+180 p^6-975 p^5+2600 p^4-3510 p^3+2184 p^2-455 p\right)-4 p+1\right) z^7+O\left(z^8\right)$$

We then set the coefficient of $z^7$ equal to zero and choose the solution for $p$ for which the absolute value of the coefficient of $z^6$ is the least. In the case at hand this also corresponds to choosing the solution for $p$ with the largest magnitude. As shown by Zinn-Justin, this choice is optimal because the mapping is proportional to $p$ and then larger $p$ leads to a larger radius of convergence. However, this logic cannot be generalized for more general conformal mappings while minimizing the modulus of the coefficient of the next largest power of $z$ will always work and will usually lead to the best choice.

We then find that the optimal solution is $p = 3.9562952014676\ldots$. If we then set $p$ to this value and put $z = 1$ in the above expansion and multiply that by $\sqrt{p}$, we find the estimate $1.5777\ldots$ for the limit. This not extremely accurate, but then we are trying to extract the value of a function at infinity from only 8 terms of a series with a radius of convergence of 1.

We can improve on this result by considering conformal transforms with more parameters and then equating the last few terms of the series to zero and picking the optimal solution as the one that minimizes the norm of the coefficient of the highest power of z that was not set to zero. However, while this does lead to very accurate results, this is a tour de force.

Obtaining a better estimate by taking linear combinations of solutions

There exists a simpler method that leads to reasonable accurate results that involves using the other solutions of the equation obtained when we set the coefficient of $z^7$ equal to zero. We then consider the linear combinations of such solutions that make the coefficients of lower powers of $z$ zero and then take the corresponding linear combinations of the estimates for the limits. For the problem at hand, this works as follows:

Let's denote the coefficient of $z^r$ by $k_r(p)$. Let $p_i$ for $0\leq i\leq 6$ be the solutions such that $|k\left(p_i\right)|$ is increasing as a function of $i$. For $n=1\cdots 6$ we compute coefficients $a^{(n)}_i$ with $1\leq i\leq n$ such that:

$$k_r\left(p_0\right)+\sum_{j =1}^n a^{(n)}_{j} k_r\left(p_j\right)=0$$

for $r = 6, 5,\cdots, 7-n$. Let's denote the series evaluated as $z = 1$ as a function of $p$ multiplied by $\sqrt{p}$ which we use to estimate the limit by $u(p)$. We then evaluate the expressions:

$$A_n = \frac{u\left(p_0\right)+\sum_{j =1}^n a^{(n)}_{j} u\left(p_j\right)}{1+\sum_{j =1}^n a^{(n)}_{j}}$$

and we put $A_0 = u\left(p_0\right)$. This yields successive approximants for the limit that at first become better and then start to become worse. We then find: $$ \begin{split} A_0 &= 1.577742424\\ A_1 &= 1.570563331\\ A_2 &= 1.570839165\\ A_3 &= 1.570774607\\ A_4 &= 1.570822307\\ A_5 &= 1.570720746\\ A_6 &= 1.571483896 \end{split} $$

The simplest way to choose the most accurate one without cheating is the look at the successive differences and choose the one where the difference with the next value is the smallest. A better way is to construct a new series:

$$h(x) = A_0 + \sum_{k = 0}^5 \left(A_{k+1}-A_k\right)x^{k+1} + \mathcal{O}\left(x^7\right)$$

which we want to evaluate at $x = 1$. We can then start a new round of the same method as we applied to the original series. If we want to use the conformal mapping method, then we must omit the $A_0$ term for the series, because we need the series coefficients to be smooth. In contrast, Padé approximants can be used directly on the series. The best Padé approximant for a series of order $2n$ is usually the diagonal $\{n,n\}$ Padé approximant. In this case we find that the $\{3,3\}$ Padé approximant is given by $1.570799\cdots$ while the exact answer is $\frac{\pi}{2}= 1.570796\cdots$.

Conclusion

The method I presented here involves applying a conformal transform containing $r$ parameters, setting the coefficients of the highest $r$ powers of $z$ equal to zero, and then choosing the that solution for which the coefficient of the highest power of $z$ that was not set to zero has the least absolute value. The enormous complexity of the equations when more than one parameter is used can be a problem. One can instead use linear combinations of the different solutions to set the coefficients of the lower powers of $z$ to zero and consider the corresponding linear combinations of the estimates.

As pointed out above, the reason why setting the highest known coefficient of $z$ to zero works well, is because this makes the summation of the known terms correspond to the optimal truncation rule, which in the theory of asymptotic expansions is known as the superasymptotic approximation, as the error is then beyond all powers of the expansion parameter.

But the reason why choosing the optimal value of the solution to be the one that minimizes the norm of the coefficient of the next highest power and why with more parameters one should set the coefficients of the next highest powers to zero needs more explanation. We can argue heuristically as follows. Suppose we have a conformal transform $x = \phi(z)$ such that the $r$ highest known series expansion coefficients of $g(z) = f\left[\phi(z)\right]$ are zero. The inverse mapping from $g(z)$ to $f(x)$ reproduces $f(x)$, but note that because the $r$ highest known powers of $z$ are zero, the $r$ highest powers of $x$ in $f(x)$ are generated using only the lower powers of $g(z)$. The coefficients of these lower powers follow in turn from the lower powers of $f(x)$.

So, the conformal mapping constructed by setting the coefficients if the $r$ highest powers of $z$ to zero, ends up being a predictive tool for the coefficients of the $r$ highest powers of $x$ of $f(x)$. what then typically happens is that the coefficients of the next powers of $x$ are very accurately reproduced when we simply assume that the coefficients of these powers of $z$ are zero in $g(z)$.

Padé approximants can also be considered in this way. Given a function $f(x)$ for which we know the series expansion up to $n$th order, we can consider the series expansion of $p(x) = q(x) f(x)$ to $n$th order for $q(x)$ an $r$th degree polynomial. We can then choose $q(x)$ such that the highest $r$ powers of $p(x)$ vanish. This thus yields the $\{n-r,r\}$ Padé approximant as

$$f(x) = \frac{p(x)}{q(x)} + \mathcal{O}\left(x^{n+1}\right)$$

Then comparing this to the order dependent mapping method, $q(x)$ is analogous to the conformal mapping and $p(x)$ is analogous to the series obtained after applying the conformal mapping. Then the analogous reasoning is that because this correctly reproduces $f(x)$ to $n$th order while the highest $$r orders if $p(x)$ are missing we can assume that setting the next highest orders of $p(x)$ to zero for the same $q(x)$ will approximately reproduce the coefficients of the powers of $f(x)$ higher than $n$ as well. This predictive power is indeed a well known feature of Padé approximants.