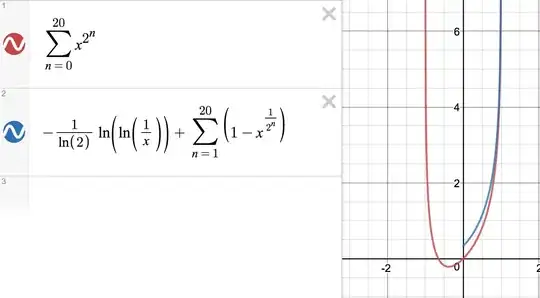Extending Lacunary Series beyond their disks

Question

I've been for the past year and half fascinated by the lacunary series $f(z) = \sum_{n=0}^{\infty} z^{2^n}$. This function obeys the following equation inside the unit disk.

$$f(z^2) = f(z)-z$$

And there is no known "natural" way to extend the function outside the disk, so I attempted to create a way. Consider now the following formula.

$$ G(x)= - \frac{1}{\ln(2)} \ln\ln x + \left(1 - \sqrt{x}\right) + \left( 1 - \sqrt{\sqrt{x}} \right)+ \left(1- \sqrt{\sqrt{\sqrt{x}}} \right) ... $$

It's clear that $G(x^2) = G(x) - x$, and moreover it's well defined over $\mathbb{R}^+ - \lbrace 0,1\rbrace$. If we consider $0 < x < 1$

$$G(x) = - \frac{i \pi}{\ln(2)} - \frac{1}{\ln(2)} \ln\ln \frac{1}{x} + \left(1 - \sqrt{x}\right) + \left( 1 - \sqrt{\sqrt{x}} \right)+ \left(1- \sqrt{\sqrt{\sqrt{x}}} \right) ... $$

So you can graph $G(x) + \frac{i \pi}{\ln(2)} $, and observe it as a function, compared to the lacunary series above

Clearly the graphs are extremely similar. And it's not hard to see that $w(x) = g(x)-f(x)$ obeys the functional equation $w(x^2) = w(x)$.

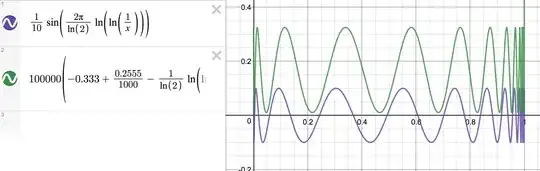
After taking the difference of the two graphs, it looks nearly constant but some careful inspection reveals that $w$ has non trivial structure and its first terms are

$$ \frac{i \pi}{\ln(2)} + w(x) \approx 0.333 + \frac{0.255}{1000} + c_0 \sin \frac{2\pi}{\ln 2} \ln \ln \frac{1}{x}... $$

Where $c_0 \approx 10^{-4}$ see below for visual evidence

So naturally one can use a variant of fourier analysis to come up with sequences of complex numbers $a_k, b_l$ such that:

$$w(x) + \frac{i \pi}{\ln(2)} = c + \sum_{k=0}^{\infty} a_k \sin \frac{2\pi}{\ln 2} \ln \ln \frac{1}{x} + \sum_{l=0}^{\infty} b_l \sin \frac{2\pi}{\ln 2} \ln \ln \frac{1}{x} $$

And therefore:

$$ -\frac{\ln \ln x }{\ln(2)} + \sum_{n=1}^{\infty} \left( 1 - x^{\frac{1}{2^n}} \right) - \frac{i \pi}{\ln(2)} - c - \sum_{k=0}^{\infty} \left( a_k \sin \frac{2\pi}{\ln 2} \ln \ln \frac{1}{x} \right) - \sum_{l=0}^{\infty} \left( b_l \sin \frac{2\pi}{\ln 2} \ln \ln \frac{1}{x} \right) = \sum_{n=0}^{\infty} x^{2^n} $$

Over $0 < x < 1$ (call the entire completed left hand side $L$ noting that $L = G(x) - w(x)$). Now it's interesting observe that $L$ is a complex function defined over all real positive numbers, and $L(x^2) = L(x) -x $ over the entire line. We CAN extend $L$ to the entirety of the complex plane using that functional equation and using the values of $L$ on the real line, leading us to create $L(z)$ defined globally on the plane minus the unit disc.

Some natural questions arise then:

1. Can we prove that as $x \rightarrow 0$ our definition of $L$ approaches 0? It's clear with the many nested-log-terms that $L$ is not defined at $x=0$ but if a limit can nevertheless be assigned it would be nice since we can then have $L$ agree with $f(z)$ over the entire open unit disk.

2. "What nice properties" does $L$ extended to the complex plane have? Is it continuous, is it locally analytic, etc...?

3. We define $L$ through its functional equation for complex arguments, but the series form of $L$ has 3 countably long sequences of functions. Is it possible to select branch cuts for each function in such as way, as to allow $L$ to be directly evaluated from its formula over complex values? (Instead of resorting to the functional equation).

4. There's a nice result from the 1980s that lacunary series such as the one above don't have unique continuous or even unique locally analytic extensions. Nevertheless, if (3) is successful, then if one looks at $L$ it has a "nice" decomposition, meaning it is built using rather elementary or simply behaved functions. This motivates the following question, is there a subset of locally-analytic functions that can be defined (Call them R-functions) so that all "analytic continuations" are also unique R continuations, and moreover the series I have given above is the unique R continuation of the lacunary series $f(z)$?

I've been ruminating on this result for a while and I needed a place to put my questions out in the public domain, to collect feedback. My blog has a total viewership of maybe 3 people, so posting this on stackexchange seemed like a more appropriate venue.

Updates:

The fourier series was explored alongside Bill Gosper and we found a few terms: https://www.wolframcloud.com/objects/637b5c6b-f016-43e1-8d1e-935506bb4d24, there are more written up if anyone wants I can provide.

Discussions with Noam Elkies and Warren Smith revealed that these series are known in the past, but its no longer clear if the coefficents decay fast enough to enable convergence outside the disc. This exercise might just reduce to pretty new identity.

Answer 1

If the functional equations that are valid for $f(z)$ still hold for its continuation, then it won't be continuous outside the unit disk. Consider the difference of $f(z)$ for 2 close points: $$ f\left(z e^{\frac{2\pi i}{2^N}}\right)-f(z)=\sum_{n=0}^N\left(e^{\frac{2\pi i}{2^{N-n}}}-1\right)z^{2^n}=\left(e^{\frac{2\pi i}{2^{N}}}-1\right)z+\ldots+(i-1)z^{2^{N-2}}+((-1)-1)z^{2^{N-1}} $$ For large $N$ and $|z|<1$, the right-hand side is small: the first terms are small because $e^{\alpha}\approx 1$ for small $\alpha$, and the last terms are small because of $z$ in a large power. This is expected result because is $f(z)$ is continuous inside the disk $|z|<1$: $$ z e^{\frac{2\pi i}{2^N}}\rightarrow z,\; f\left(z e^{\frac{2\pi i}{2^N}}\right)\rightarrow f(z)\;\textrm{when}\;N\rightarrow\infty $$ However, if $|z|>1$, the last term of the right-hand side dominates: $$ f\left(z e^{\frac{2\pi i}{2^N}}\right)-f(z)\approx -2z^{2^{N-1}}\rightarrow \infty \;\textrm{when}\;N\rightarrow\infty$$ It means that $f(z)$ is not continuous for all points $|z|>1$, and it is unbounded in the vicinity of every point.