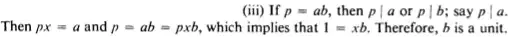In a integral domain every prime element is irreducible

Question

I'm trying to understand a proof of Hungerford's book which says that in a integral domain every prime element is irreducible:

I didn't understand why this implication $p=ab\implies p|a$ or $p|b$, is not the contrary $p=ab\implies a|p$ and $b|p$ ?

I'm a little confused

Thanks in advance

Answer 1

If $p = ab$, then in particular $p$ divides $ab$, because $ab = p \cdot 1$. Since $p$ is prime, it has to divide either $a$ or $b$.

Answer 2

Prime $\Rightarrow$ irreducible is obvious if we employ a definition of irreducible in associate (vs. $\rm\color{#0a0}{unit}$) form. Then $\,\color{#c00}{ p=ab\,\Rightarrow\, p\mid ab}\,$ immediately yields the sought inference, as follows.

Theorem $\ \ $ In the following, $\,\ (1)\,\Rightarrow\,(2)\!\iff\! (3)$

$(1)\ \ \ \color{#c00}{p\ \mid\ ab}\ \Rightarrow\ p\:|\:a\ \ {\rm or}\ \ p\:|\:b\quad$ [Definition of $\:p\:$ is prime]

$(2)\ \ \ \color{#c00}{p=ab}\ \Rightarrow\ p\:|\:a\ \ {\rm or}\ \ p\:|\:b\quad$ [Definition of $\:p\:$ is irreducible, in associate form]

$(3)\ \ \ p=ab\ \Rightarrow\ a\:|\:1\ \ {\rm or}\ \ b\:|\:1\quad$ [Definition of $\:p\:$ is irreducible, in $\rm\color{#0a0}{unit}$ form]

Proof $\ \ \ (1\Rightarrow 2)\,\ \ \ \color{#c00}{p = ab\, \Rightarrow\, p\mid ab}\,\stackrel{(1)}\Rightarrow\,p\mid a\:$ or $\:p\mid b.\ $ Hence prime $\Rightarrow$ irreducible.

$(2\!\!\iff\!\! 3)\ \ \ $ If $\:p = ab\:$ then $\:\dfrac{1}b = \dfrac{a}p\:$ so $\:p\:|\:a\iff b\:|\:1.\:$ Similarly $\:p\:|\:b\iff a\:|\:1.$

Beware that factorization theory is more complicated in non-domains. Basic notions such as associate and irreducible bifurcate into a few inequivalent notions. See here for more on that.

Answer 3

I think the OP was asking why the first implication is there instead of the alternate implication he proposed. The answer is that the first implication is part of the definition of a prime. Look at the definition of prime that precedes the theorem in question in Hungerford: An element p of R is prime provided that: (i) p is a nonzero non unit; (ii) p|ab $\Rightarrow$ p|a or p|b.

Answer 4

Let $R$ be an integral domain and let $(p) \subset R$ be prime. We claim $p$ is irreducible.

Put

$$p = ab$$

And it’s enough to show either $a$ or $b$ is a unit. It’s clear that

$$ab \in (p)$$

But $(p)$ is prime so $a \in (p)$ or $b \in (p)$. So without any loss of generality suppose that $a \in (p)$ then there exists an $r \in R$ such that

$$a=pr \Rightarrow p = prb$$

By cancellation we conclude $rb=1$ thus $b$ is a unit and $p$ is irreducible.