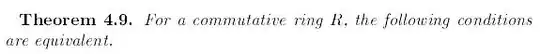1

I am taking following definitions and calling algebraic structure U1 and U2 definition as:

U1 is A ring R with unity and properties properties

  1. Every element of R is neither 0 nor a unit can be factored into a product of finite no. of primes

  2. And factorization unique upto associates.

U2 is A ring R with unity and properties properties

  1. Every element of R is neither 0 nor a unit can be factored into a product of finite no. of irreducible

  2. And factorization unique upto associates.

Are U1 and U2 equivalent? What if I include commutative condition also? Does there exist structure like this? What is example of U2 which is not UFD?(if possible)

Note: a and b Associate means if a=ub or a = bv then u and v are unit

Sushil
  • 2,821
  • If factorization into irreducibles is unique, then all irreducibles are prime, and you have a UFD. Primes are always irreducibles, aren't they? – Gerry Myerson Feb 14 '15 at 12:12
  • @GerryMyerson Ya correct but would U1 imply U2 because it is ring with unity, this may not imply primes are irreducibe – Sushil Feb 14 '15 at 13:19
  • and why would it become UFD how commutativity and non-existence of zero divisors is guaranteed @GerryMyerson – Sushil Feb 14 '15 at 13:21

1 Answers1

4

First, let's consider the simpler case when $R$ is an integral domain. Part 2 of U1 is redundant since factorizations into primes are unique (up to associates and order), by the same simple proof as in $\,\Bbb Z$ (recall prime $\Rightarrow$ irreducible). Here U1 and U2 are both are equivalent to $R$ is a UFD. This follows by the standard proofs given in most any textbook on abstract algebra.

Factorization theory is more complicated in non-domains: basic notions such as associate and irreducible bifurcate into a few inequivalent notions. For a survey in the commutative case, see D.D. Anderson, and S. Valdes-Leon, $ $ Factorization in Commutative Rings with Zero-divisors. Below I have appended some of their results pertaining to your query (whose answer depends on the precise notion of "associate" and "irreducible" that is employed).

For noncommutative UFDs it is more convenient to employ refinement-based views of unique factorization, e.g. see Paul Cohn's 1973 Monthly survey Unique factorization domains. and see also his 1963 TAMS paper Noncommutative unique factorization domains.

enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here enter image description here

Community
  • 1
Bill Dubuque
  • 272,048