In the ${\Bbb P}^5$ of coefficients $(a:b:c:d:e:f)$ for the conic $ax^2+bxy+cy^2+dxz+eyz+fz^2=0,$ going through a point is linear condition; just specify the point say $(4:1:1)$ and the condition, by substituting the point, is $16a+4b+c+4d+e+f=0.$
The condition to be tangent to given lines $a_i x+b_i y+c_i z=0$ is each of degree two. The dual conic through say $0.2 x+0.7 y+1=0,$ is again by substituting the point $(0.2:0.7:1)$ in the dual plane of lines in the plane into the dual conic of lines tangent to the original conic: $25cf+9bf+(81af)/25-(25e^2)/4-(9de)/2+5be+(18ae)/5-(81d^2)/100-10cd-(9bd)/5=0.$
(The dual conic is given by the inverse matrix (or more generally the adjugate matrix) of the matrix of the original conic.)
Now a (linear, quadratic etc) condition generally cuts away one dimension. Think of one, two, three, four, and five linear equations in five unknowns. This is why we expect five conditions to determine a finite number of conics. In addition looking at the fact that five linear conditions give $1^5$ conics through five points we might expect the number to be given by Bezout more generally.
Being a parabola is a tangency with the line at infinity $z=0,$ so for parabolas one condition of degree $2$ is taken and four more are needed to get a finite number. And for parabolas through four points we get $2\cdot 1^4$ which is correct.
Now there is a complication that I leave for the end, so that we cannot trust the Bezout numbers, like $6^5$ conics tangent (for a conic to be tangent to a conic is a degree $6$ condition on the coefficients) to five conics in general position; the actual number, famously, is $3264$.
For 2. Using the geogebra app in the answer in the linked question in my comment to the question I get $x^2-12xy+36y^2-24x-52y+144=0.$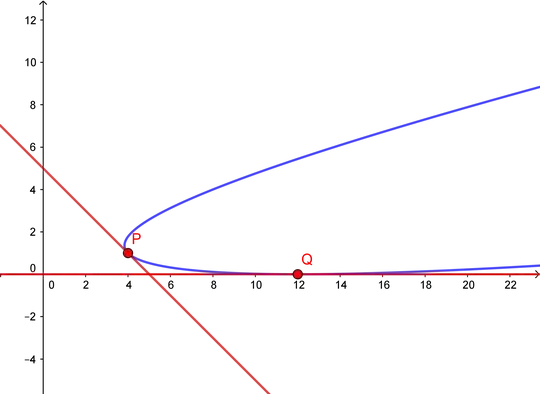 
For 1. There is an infinity of parabolas tangent to three lines. But I elect to show a way to get the unique parabola tangent to four given lines in general position.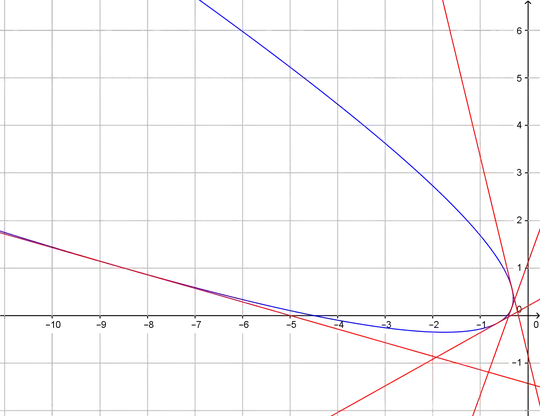 
For example, if we take the four lines to be $x X_i+y Y_i+1=0,$ where $X_1=0.2,Y_1=0.7,X_2=2.5,Y_2=-0.9,X_3=2.8,Y_3=-5,X_4=5,Y_4=1.2,$ the dual conic $afY^2-\frac14 d^2Y^2-bfXY+\frac12 deXY-aeY+\frac12 bdY+cfX^2-\frac12 e^2X^2+\frac12 beX-cdX+ac-\frac14 b^2=0$ (dual to $ax^2+bxy+cy^2+dx+ey+f=0$) evaluated at $(X_i,Y_i)$ together with the condition to be a parabola $b^2-4ac=0$ give in M2
T=QQ[a,b,c,d,e,f,MonomialOrder=>Lex]
J=ideal(25*c*f+9*b*f+(81*a*f)/25-(25*e^2)/4-(9*d*e)/2+5*b*e+(18*a*e)/5-(81*d^2)/100-10*c*d-(9*b*d)/5, (4*c*f)/25-(14*b*f)/25+(49*a*f)/25-e^2/25+(7*d*e)/25+(2*b*e)/5-(14*a*e)/5-(49*d^2)/100-(4*c*d)/5+(7*b*d)/5, (784*c*f)/25+56*b*f+100*a*f-(196*e^2)/25-28*d*e+(28*b*e)/5+20*a*e-25*d^2-(56*c*d)/5-10*b*d, 100*c*f-24*b*f+(144*a*f)/25-25*e^2+12*d*e+10*b*e-(24*a*e)/5-(36*d^2)/25-20*c*d+(12*b*d)/5,b^2-4*a*c)
gens gb J
primaryDecomposition radical J
toString oo -- {ideal(4*c*f-e^2,2*b*f-d*e,b*e-2*c*d,4*a*f-d^2,2*a*e-b*d,4*a*c-b^2),
ideal(98051402514954215*e+85617834771997822*f,
19610280502990843*d-49279136609744940*f,
490257012574771075*c-1031289706001844147*f,
19610280502990843*b-40544108165505524*f,
58830841508972529*a-29886571227928900*f)}
If we let $f=1,$ clear denominators, and factor the coefficients, the unique solution parabola is $(2\cdot 5^2\cdot 17287733\cdot x+3\cdot 1013\cdot 578789\cdot y)^2+2^2\cdot 3^2\cdot 5^3\cdot 79\cdot 10396442322731\cdot x-2\cdot 3\cdot 5\cdot 7\cdot 113\cdot 54119996695321\cdot y+3\cdot 5^2\cdot 97\cdot 971\cdot 98731\cdot 2108819=0.$
Now, the problem is interesting in intersection theory, because the Veronese of double lines (ideal(4*c*f-e^2,2*b*f-d*e,b*e-2*c*d,4*a*f-d^2,2*a*e-b*d,4*a*c-b^2) above) appears. This is why the Bezout answer to how many conics are tangent to five lines (there are five degree two conditions; so $2^5$) is wrong, beacuse there's excess intersection and the equivalent of the double lines amounts to $31$ (Fulton Intersection Theory Example 9.1.8).
