This can be recasted into the so-called "Newton's problem" as treated here : http://www2.washjeff.edu/users/mwoltermann/Dorrie/45.pdf where it is shown that a parabola (in fact two of them) can pass through 4 points
Condition ($C_1$): the 4 points form a convex quadrilateral.
As a consequence, let $T$ be the "filled" triangle formed by the three initial points. Then condition ($C_1$) is equivalent to
Condition ($C_2$): [There is a parabola through the 3 first points and the fourth point] if and only if the fourth point is in the complementary set of the forbidden red region represented in the following figure (triangle $T$ + $3$ spiky regions).
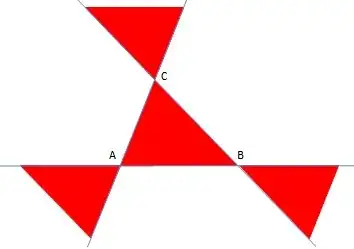
Fig. 1: Forbidden regions for the fourth point (in red)._
Remark : I am very indebted to Oscar Lanzi who has pointed an error of mine about condition $(C_2)$ in a previous formulation ; moreover, he has pointed the exceptional case where the points form a parallelogram: in this case, the parabola(s) are degenerated into 2 parallel lines.
$(C_2)$ is equivalent to the following condition:
Condition $(C_3)$: the barycentrical coordinates of the fourth point must have two positive and one negative component.
As a consequence, $(C_3)$ is equivalent to:
Condition $(C_4)$: [There is a parabola through the 3 first points and the fourth point] if and only if
$$\dfrac{\begin{vmatrix}x_4&x_2&x_3\\ y_4&y_2&y_3\\1&1&1\end{vmatrix}\begin{vmatrix}x_1&x_4&x_3\\ y_1&y_4&y_3\\ 1&1&1\end{vmatrix}\begin{vmatrix}x_1&x_2&x_4\\ y_1&y_2&y_4\\ 1&1&1\end{vmatrix}}{\begin{vmatrix}x_1&x_2&x_3\\ y_1&y_2&y_3\\ 1&1&1\end{vmatrix}^3}\color{red}{<0}$$
(Exponent 3 can be suppressed.)
This may be rendered into the form of a symmetric product of determinants:
$$\begin{vmatrix}x_1&x_2&x_3\\ y_1&y_2&y_3\\1&1&1\end{vmatrix}\begin{vmatrix}x_2&x_3&x_4\\ y_2&y_3&y_4\\ 1&1&1\end{vmatrix}\begin{vmatrix}x_3&x_4&x_1\\ y_3&y_4&y_1\\ 1&1&1\end{vmatrix}\begin{vmatrix}x_4&x_1&x_2\\ y_4&y_1&y_2\\ 1&1&1\end{vmatrix}\color{red}{>0}$$
The sign change comes from the fact that some pairs of columns were interchanged to put the determinants into the symmetric form..
Remark about the reference given above: M. Woltermann (Washington and Jefferson College) has undertook a huge task: providing a digital version of the famous book "One Hundred great Problems of Mathematics" originaly published in german in 1932 by Heinrich Dörrie, meanwhile (intelligently) grooming it. This explains in particular the last sentence mentionning an alternative projective method that indeed can be found in the original version of the book p. 208 n°45 here.
A very detailed analysis of the Newton's problem can be found here.
Section under development: I have attempted to develope my own projective proof using the fact that it is always possible to give a parabola the following parametric equations:
$$x=\tfrac{at^2+bt+c}{t-d}, \ \ \ y=\tfrac{et^2+ft+g}{t-d} \tag{1}$$
(a hint for getting intuition about (1): when $t=d$, one has the unique point at infinity of the parabola).
Please note that there are $7$ unknowns, $a,b,c,d,e,f,g$.
Constraining a fourth point to belong to this parabola works on numerical examples but I have some difficulty to find a general justification.
